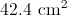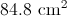How to find the area of a sector
Help Questions
Math › How to find the area of a sector
Find the area of the sector that has a central angle of 

Explanation
The circle in question can be drawn as shown by the figure below:

Since the area of a sector is just a fractional part of the area of a circle, we can write the following equation to find the area of a sector:


Plug in the given central angle and radius to find the area of the sector.
Make sure to round to two places after the decimal.
Find the area of a sector with a central angle of 

Explanation
The circle in question could be depicted as shown in the figure.

Recall the formula for finding the area of a sector of a circle:
Since the central angle and the radius are given in the question, plug them in to find the area of the sector.
Solve and round to two decimal places.
Find the area of a sector if it has an arc length of 

The area of the sector cannot be determined.
Explanation
The length of the arc of the sector is just a fraction of the arc of the circumference. The area of the sector will be the same fraction of the area as the length of the arc is of the circumference.
We can then write the following equation to find the area of the sector:
The equation can be simplified to the following:
Plug in the given arc length and radius to find the area of the sector.
Find the area of the following sector:

Explanation
The formula for the area of a sector is

where 

Plugging in our values, we get:
Find the area of the shaded region:

Explanation
To find the area of the shaded region, you must subtract the area of the triangle from the area of the sector.
The formula for the shaded area is:

where 



In order to the find the base and height of the triangle, use the formula for a 



Plugging in our final values, we get:
To the nearest tenth, give the area of a 
Explanation
The radius of a circle with diameter 18 centimeters is half that, or 9 centimeters. The area of a 
Find the area of a sector that has a central angle of 

Explanation
The circle in question can be drawn as shown by the figure below:

Since the area of a sector is just a fractional part of the area of a circle, we can write the following equation to find the area of a sector:


Plug in the given central angle and radius to find the area of the sector.
Make sure to round to two places after the decimal.
Find the area of a sector if it has an arc length of 

Explanation
The length of the arc of the sector is just a fraction of the arc of the circumference. The area of the sector will be the same fraction of the area as the length of the arc is of the circumference.
We can then write the following equation to find the area of the sector:
The equation can be simplified to the following:
Plug in the given arc length and radius to find the area of the sector.
Find the area of a sector that has a central angle of 

Explanation
The circle in question could be depicted as shown in the figure.

Recall the formula for finding the area of a sector of a circle:
Since the central angle and the radius are given in the question, plug them in to find the area of the sector.
Solve and round to two decimal places.
Find the area of a sector that has a central angle of 

Explanation
The circle in question can be drawn as shown by the figure below:

Since the area of a sector is just a fractional part of the area of a circle, we can write the following equation to find the area of a sector:


Plug in the given central angle and radius to find the area of the sector.
Make sure to round to two places after the decimal.