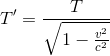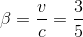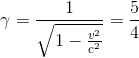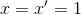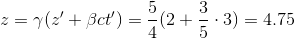Special Relativity
Help Questions
GRE Subject Test: Physics › Special Relativity
At one point in time, two twins are 30 years old. At this time, one of them gets on a rocket and travels at 0.8 c, for what he experiences to be 12 years. How old is the twin that remained on Earth when the traveling twin returns home?
50 years old
37 years old
42 years old
70 years old
Explanation
The equation for time dilation is given by:
In this problem v=0.8c T=12. Using this equation, we get:
Adding 20 years to the age initial age of 30:
The Earth-twin is now 50.
A reference frame S' is moving at 0.6_c_ in the z direction with respect to a stationary frame S. An event occurs in S' with the coordinates (x', y', z', ct')=(1, 0, 2, 3). What are the coordinates (x, y, z, ct) of the event with respect to the stationary frame S?
(1, 0, 4.75, 5.25)
(1, 0, 5.25, 4.75)
(1, 0, 2.64, 3.3)
(1, 0, 3.3, 2.64)
(1, 0, 2, 3)
Explanation
To apply a Lorentz transformation, we need gamma and beta:
Then, apply the Lorentz transformation:
A black hole is an object whose gravitational field is so strong that even light cannot escape. Assuming no change in radius, approximately how much mass would our Sun have to have in order to become a black hole?
Sun's radius:
Explanation
To derive the Schwarzschild radius of a black hole, set gravitational potential energy equal to kinetic energy at escape velocity:
Solving for mass of the black hole:
The difference in age for the twins in the Twin Paradox occurs during which key moment in the trip?
During the period of great acceleration during the changing of directions and return to Earth.
During the beginning of the journey traveling fast.
During the time returning to Earth traveling fast.
While approaching a black hole in space during the trip.
None of these
Explanation
While moving clocks do in fact record time moving at different rates, the time dilation works both ways. This means that a stationary person will view a moving clock ticking slower, but at the same time, a person moving alongside the moving clock will see the stationary clock ticking slower. However, clocks experiencing great accelerations will be permanently changed, "losing" time relative to a clock not being accelerated. Thus, the age difference occurs during the portion of the journey when the traveler accelerates at a great rate in order to return to Earth.
A rocket of length 5 meters passes an observer on earth. The observer measures the passing rocket to be 3 meters long. What is the velocity of the rocket in the reference frame of the Earth-based observer?
Explanation
Length contraction is given by
Where in this case,
The Lorentz factor is given by:
Combining these two equations, we get:
Solving for v:
A rocket of length 5 meters passes an observer on earth. The observer measures the passing rocket to be 3 meters long. What is the velocity of the rocket in the reference frame of the Earth-based observer?
Explanation
Length contraction is given by
Where in this case,
The Lorentz factor is given by:
Combining these two equations, we get:
Solving for v:
A relativistic particle of mass m has a total energy 37 times its rest energy. What is the momentum of the particle, in units of mc?
37
52
98
21
144
Explanation
The total energy E of a relativistic particle is related to its rest mass energy Eo by:
Where gamma is related to the momentum by:
Combining the equations and solving for p, we get:
Which, in the units specified, is 37.
A black hole is an object whose gravitational field is so strong that even light cannot escape. Assuming no change in radius, approximately how much mass would our Sun have to have in order to become a black hole?
Sun's radius:
Explanation
To derive the Schwarzschild radius of a black hole, set gravitational potential energy equal to kinetic energy at escape velocity:
Solving for mass of the black hole:
The difference in age for the twins in the Twin Paradox occurs during which key moment in the trip?
During the period of great acceleration during the changing of directions and return to Earth.
During the beginning of the journey traveling fast.
During the time returning to Earth traveling fast.
While approaching a black hole in space during the trip.
None of these
Explanation
While moving clocks do in fact record time moving at different rates, the time dilation works both ways. This means that a stationary person will view a moving clock ticking slower, but at the same time, a person moving alongside the moving clock will see the stationary clock ticking slower. However, clocks experiencing great accelerations will be permanently changed, "losing" time relative to a clock not being accelerated. Thus, the age difference occurs during the portion of the journey when the traveler accelerates at a great rate in order to return to Earth.
A reference frame S' is moving at 0.6_c_ in the z direction with respect to a stationary frame S. An event occurs in S' with the coordinates (x', y', z', ct')=(1, 0, 2, 3). What are the coordinates (x, y, z, ct) of the event with respect to the stationary frame S?
(1, 0, 4.75, 5.25)
(1, 0, 5.25, 4.75)
(1, 0, 2.64, 3.3)
(1, 0, 3.3, 2.64)
(1, 0, 2, 3)
Explanation
To apply a Lorentz transformation, we need gamma and beta:
Then, apply the Lorentz transformation: