Calculating the area of an acute / obtuse triangle
Help Questions
GMAT Quantitative › Calculating the area of an acute / obtuse triangle
What is the area of a triangle on the coordinate plane with its vertices on the points 
Explanation
The vertical segment connecting 





Which of the following is the area of a triangle on the coordinate plane with its vertices on the points 

Explanation
We can view the horizontal segment connecting 






What is the area, to the nearest whole square inch, of a triangle with sides 12, 13, and 15 inches?
None of the other answers are correct.
Explanation
Use Heron's formula:
where 
What is the area of the triangle on the coordinate plane formed by the 


Explanation
The easiest way to solve this is to graph the three lines and to observe the dimensions of the resulting triangle. It helps to know the coordinates of the three points of intersection, which we can do as follows:
The intersection of 


The lines intersect at
The intersection of 

These lines intersect at
The intersection of 

The lines intersect at
The triangle therefore has these three vertices. It is shown below.

As can be seen, it is a triangle with base 9 and height 12, so its area is

Note: Figure NOT drawn to scale.
What is the area of the above figure?
More information is needed to answer this question.
Explanation
The figure is a composite of a rectangle and a triangle, as shown:

The rectangle has area
The triangle has area
The total area of the figure is
Give the area of a triangle on the coordinate plane with vertices 
Explanation
This can be illustrated by showing this triangle inscribed inside a rectangle whose vertices are 

The area of the white triangle 
The area of the red triangle:
The area of the green triangle:
And the area of the beige triangle:
The area of the white triangle will be as follows:
Calculate the area of the triangle (not drawn to scale).
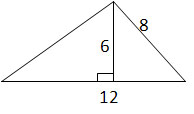
Explanation
In this problem, the base is 12 and the height is 6. Therefore:
Which of the following cannot be the measure of the vertex angle of an isosceles triangle?
Each of the other choices can be the measure of the vertex angle of an isosceles triangle.
Explanation
The only restriction on the measure of the vertex angle of an isosceles triangle is the restriction on any angle of a triangle - that it fall between 



Since all of these measures fall in that range, the correct response is that all are allowed.




































































