Similar Triangles and Proportions
Help Questions
GED Math › Similar Triangles and Proportions
In the figure below, the two triangles are similar. Find the value of 

Explanation
Since the two triangles are similar, we know that their corresponding sides must be in the same ratio to each other. Thus, we can write the following equation:
Now, solve for 
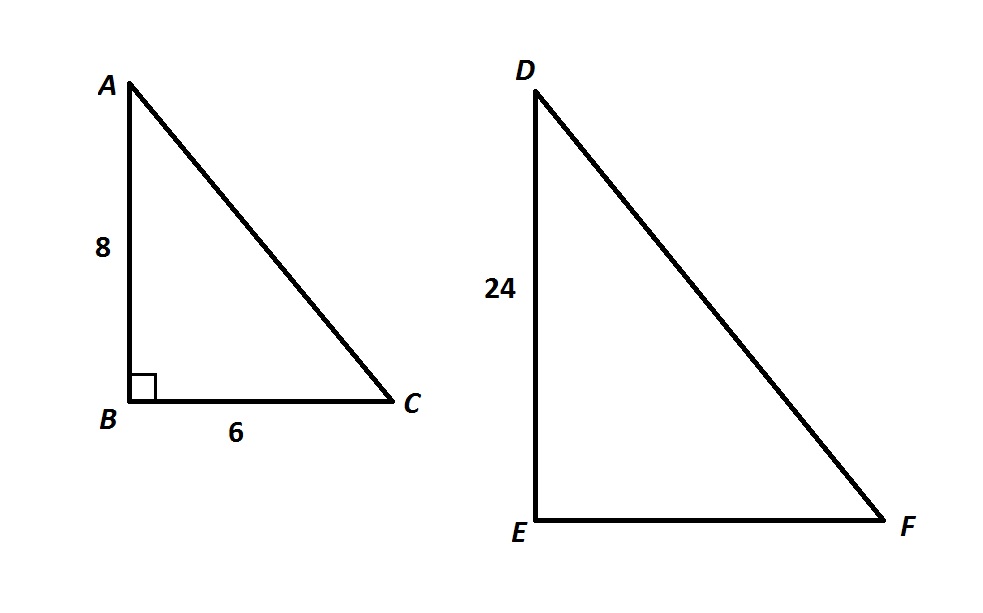
Note: Figure NOT drawn to scale.
Refer to the above diagram. If 

Explanation
Suppose 
Corresponding angles of similar triangles are congruent, so 



Corresponding sides of similar triangles are in proportion. Since

the similarity ratio of 

By the Pythagorean Theorem, since 



But 

Which of the following statements is not a consequence of the statement

Explanation






However, similar triangles need not have congruent corresponding sides. Therefore, it does not necessarily follow that 
Which of the following statements follows from the statement 
Explanation
The similarity of two triangles implies nothing about the relationship of two angles of the same triangle. Therefore, 
The similarity of two triangles implies that corresponding angles between the triangles are congruent. However, because of the positions of the letters, 






Similarity of two triangles does not imply any congruence between sides of the triangles, so 
Similarity of triangles implies that corresponding sides are in proportion. 







Note: Figures NOT drawn to scale.
Refer to the above figures. Given that 

Explanation
By the Pythagorean Theorem, since 

The similarity ratio of 


Likewise,

Note: Figures NOT drawn to scale.
Refer to the above figures. Given that 

Explanation
Corresponding angles of similar triangles are congruent, so, since 



By the Pythagorean Theorem, since 

The similarity ratio of 


This can be used to find 

The area of 



































