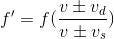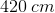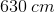Waves
Help Questions
Physics › Waves
Suppose that car A and car B are both traveling in the same direction. Car A is going 


Note: The speed of sound in air is 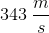
Explanation
The important concept being tested in this question is the Doppler effect. When a source of sound waves (or any other wave) is emitted from a source and is moving relative to some observer, the actual frequency of the wave will be different for the observer.
For starters, we'll need to use the Doppler equation.
The trickiest part about this question is to decide whether to add or subtract in both the numerator and denominator. To find the right sign orientation, it's helpful to do a quick thought experiment. Imagine that only one of them is moving and the other is stationary. Decide how that will affect the observed frequency; will it increase it or decrease it? Then repeat for the other one.
First, let's consider the detector (aka observer). We're told that car B, the detector, is traveling ahead of car A and also in the same direction. This means that car B is driving away from car A. So in this situation, is the frequency that car B hears expected to increase or decrease? The answer is that it will decrease. Since car B is traveling away from car A, each successive wave will take longer to reach car B. Hence, we will use subtraction in the numerator because that will make the observed frequency smaller.
Now let's apply this same logic to the denominator, which deals with the source of the sound waves. We know that car A is traveling in the same direction as car B and is behind. This means that car A is traveling toward car B. So from this perspective, each successive wave is expected to get closer together, thus making the time between each wave smaller and the frequency bigger. In the denominator, will adding or subtracting make the observed frequency bigger? The answer is subtraction. By making a smaller number in the denominator, the entire fraction becomes larger.
Keeping this information in mind, we'll need to use subtraction in both the numerator and denominator. Once we plug in the values given in the question stem, we have everything we need to solve for the answer.
When a ray of light is reflected off of the surface of another medium, some of the energy from the light is transferred into this medium. As a result, which of the following is true about the reflected light ray?
It has a lower frequency and a higher wavelength
It has a lower frequency and a lower wavelength
It has a higher frequency and a higher wavelength
It has a higher frequency and a lower wavelength
Explanation
For this question, we're told that light is reflected off of the surface of another medium. As a result, the light loses some of its energy, which is transferred into the medium where it reflected.
Because the light has lost some of its energy, we need to determine how the wavelength and frequency of the wave will be affected. To do this, we can recall the equation for the energy of a wave.
Where 

To see how the wavelength changes, it's important to recall the relationship that wavelength and frequency have with each other.
Where 

So, in summary, when the energy of light decreases, the frequency will decrease and the wavelength will increase.
Suppose that the fifth harmonic of a standing wave contained within a pipe closed at both ends has a wavelength of 
Explanation
For this question, we're told that a standing wave is contained within a pipe closed at both ends. We're also given the wavelength for the fifth harmonic, and are asked to find the length of the pipe.
The first step to solve this problem is to use the equation for a pipe closed at both ends.
Since we're told which harmonic the wave is on, as well as its wavelength, we have everything we need to solve for the length of the pipe.
When a ray of light is reflected off of the surface of another medium, some of the energy from the light is transferred into this medium. As a result, which of the following is true about the reflected light ray?
It has a lower frequency and a higher wavelength
It has a lower frequency and a lower wavelength
It has a higher frequency and a higher wavelength
It has a higher frequency and a lower wavelength
Explanation
For this question, we're told that light is reflected off of the surface of another medium. As a result, the light loses some of its energy, which is transferred into the medium where it reflected.
Because the light has lost some of its energy, we need to determine how the wavelength and frequency of the wave will be affected. To do this, we can recall the equation for the energy of a wave.
Where 

To see how the wavelength changes, it's important to recall the relationship that wavelength and frequency have with each other.
Where 

So, in summary, when the energy of light decreases, the frequency will decrease and the wavelength will increase.
Suppose that car A and car B are both traveling in the same direction. Car A is going 


Note: The speed of sound in air is 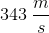
Explanation
The important concept being tested in this question is the Doppler effect. When a source of sound waves (or any other wave) is emitted from a source and is moving relative to some observer, the actual frequency of the wave will be different for the observer.
For starters, we'll need to use the Doppler equation.
The trickiest part about this question is to decide whether to add or subtract in both the numerator and denominator. To find the right sign orientation, it's helpful to do a quick thought experiment. Imagine that only one of them is moving and the other is stationary. Decide how that will affect the observed frequency; will it increase it or decrease it? Then repeat for the other one.
First, let's consider the detector (aka observer). We're told that car B, the detector, is traveling ahead of car A and also in the same direction. This means that car B is driving away from car A. So in this situation, is the frequency that car B hears expected to increase or decrease? The answer is that it will decrease. Since car B is traveling away from car A, each successive wave will take longer to reach car B. Hence, we will use subtraction in the numerator because that will make the observed frequency smaller.
Now let's apply this same logic to the denominator, which deals with the source of the sound waves. We know that car A is traveling in the same direction as car B and is behind. This means that car A is traveling toward car B. So from this perspective, each successive wave is expected to get closer together, thus making the time between each wave smaller and the frequency bigger. In the denominator, will adding or subtracting make the observed frequency bigger? The answer is subtraction. By making a smaller number in the denominator, the entire fraction becomes larger.
Keeping this information in mind, we'll need to use subtraction in both the numerator and denominator. Once we plug in the values given in the question stem, we have everything we need to solve for the answer.
Suppose that the fifth harmonic of a standing wave contained within a pipe closed at both ends has a wavelength of 
Explanation
For this question, we're told that a standing wave is contained within a pipe closed at both ends. We're also given the wavelength for the fifth harmonic, and are asked to find the length of the pipe.
The first step to solve this problem is to use the equation for a pipe closed at both ends.
Since we're told which harmonic the wave is on, as well as its wavelength, we have everything we need to solve for the length of the pipe.
A pipe has a length of 

Explanation
Since the pipe is open at both ends, we can use the equation 


We know from the question that:
When we plug in these values into the frequency equation, we get 
A pipe has a length of 

Explanation
Since the pipe is open at both ends, we can use the equation 


We know from the question that:
When we plug in these values into the frequency equation, we get 
A 
Explanation
Each harmonic has a wavelength that behaves according to the equation



Since this is the 5th harmonic, 


A 
Explanation
Each harmonic has a wavelength that behaves according to the equation



Since this is the 5th harmonic,