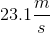Continuity Equation
Help Questions
Physics › Continuity Equation
Fluid flows into a pipe with a diameter of 


Explanation
This question tests the concept of the continuity equation which stipulates that at steady state the volume flowing into one end of a pipe must be exactly equal to the volume flowing out of the other end. That is, 
If the radius of a pipe with flowing liquid is decreased by a factor of 
Increase by a factor of
Dcrease by a factor of
Increase by a factor of
Decrease by a factor of
Explanation
To see how a change of radius affects the velocity of a moving fluid, we'll need to take the continuity equation into account.
Even though the radius is not shown in the above expression, remember that area is related to radius.
Or put another way:
When substituted into the continuity equation:
As the above proportionality shows, if the radius were to decrease by a factor of