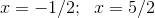Rational Functions
Help Questions
College Algebra › Rational Functions
Which is a vertical asymptote of the graph of the function

(a)
(b)
(a) only
(b) only
Neither (a) nor (b)
Both (a) and (b)
Explanation
The vertical asymptote(s) of the graph of a rational function such as 
First, factor the numerator and denominator.
The numerator is a perfect square trinomial and can be factored as such:
The denominator can be factored as the difference of squares:
Rewrite
as
The expression can be reduced by cancelling 
Set the denominator equal to 0 and solve:
The only vertical asymptote is therefore the line of the equation 
Which is a vertical asymptote of the graph of the function 
(a)
(b)
(b) only
(a) only
Neither (a) nor (b)
Both (a) and (b)
Explanation
The vertical asymptote(s) of the graph of a rational function such as 

The graph of the line 

Which of the following is a vertical asymptote of the graph of the function 
(a)
(b)
Neither (a) nor (b)
Both (a) and (b)
(b) only
(a) only
Explanation
The vertical asymptote(s) of the graph of a rational function such as 
First, factor the numerator. It is a quadratic trinomial with lead term 
We seek two integers whose sum is 


Therefore, 
Cancelling 
which does not have a vertical asymptote.
Give the equation(s) of the vertical asymptote(s) of the graph of the function


The graph of 
Explanation
The vertical asymptote(s) of the graph of a rational function such as 
Set the denominator equal to 0 and solve for 
The only vertical asymptote of the graph is the line of the equation 
Find all horizontal and vertical asymptotes in the graph of 
Horizontal asymptote at y=1
Vertical asymptote at x=3
Horizontal asymptote at y=1
Vertical asymptote at x=0
Horizontal asymptote at y=0
Vertical asymptote at x=-3
Horizontal asymptote at x=0
Vertical asymptote at y=3
None of these.
Explanation
To find vertical asymptotes, factor each quadratic and then simplify.
The vertical asymptotes are the zeros of the denominator, so x=3 is a vertical asymptote.
Horizontal asymptotes are found by analyzing the coefficients of the first term in each equation. The line 
Give the 


The graph of 

Explanation
The 




The value of the denominator here is 0, so 


Where are the vertical asymptotes of this rational function?
the function has no vertical asymptotes.
Explanation
The vertical asymptotes of a rational function are always the zeroes of the polynomial in the denominator. So to solve this problem all we need to do is find the zeroes of 
We can use the quadratic formula, 

And we get the two roots, 
Give the 


The graph of 

Explanation
The 







A fraction is equal to 0 if and only if the numerator is equal to 0, so set
Factor out 
By the Zero Product Property, one of the factors must be equal to 0, so either
or
in which case

However, setting