Graphing Polynomials
Help Questions
College Algebra › Graphing Polynomials
If the function 

Explanation
The function 



To translate along the y-axis, we use the function 

Which of the following graphs matches the function 





Explanation
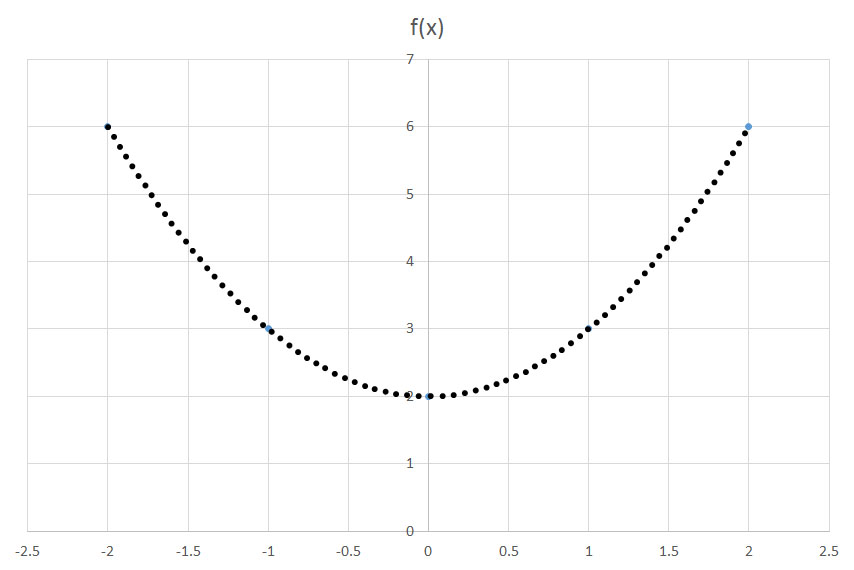
Start by visualizing the graph associated with the function 

Terms within the parentheses associated with the squared x-variable will shift the parabola horizontally, while terms outside of the parentheses will shift the parabola vertically. In the provided equation, 2 is located outside of the parentheses and is subtracted from the terms located within the parentheses; therefore, the parabola in the graph will shift down by 2 units. A simplified graph of 

Remember that there is also a term within the parentheses. Within the parentheses, 1 is subtracted from the x-variable; thus, the parabola in the graph will shift to the right by 1 unit. As a result, the following graph matches the given function 

Let 

True or false: It follows that 

True
False
Explanation
By the Factor Theorem, 
















True or false: By the Intermediate Value Theorem, 

False
True
Explanation
As a polynomial function, the graph of 




Set 





Both are polynomial graphs fitting the given conditions, but the only the equation graphed at right has a zero on 
True or false:
The polynomial 

True
False
Explanation
One way to answer this question is as follows:
Let 



as its coefficient sum, so 




True or false: By the Intermediate Value Theorem, 

True
False
Explanation
As a polynomial function, the graph of 




Setting 








True or false:
The polynomial 

False
True
Explanation
Let 


To find this alternating sum, it is necessary to reverse the symbol before all terms of odd degree. In 


so 

How many zeroes does the following polynomial have?
Explanation







If we try the next number up, 3, we get this:


and now we need to see if 
There aren't any real numbers that square to get -5 so this has no roots. Thus, 
Which of the following graphs correctly represents the quadratic inequality below (solutions to the inequalities are shaded in blue)?





Explanation
To begin, we analyze the equation given: the base equation, 


To solve the inequality, we need to take a test point and plug it in to see if it matches the inequality. The only points that cannot be used are those directly on our parabola, so let's use the origin 
Simplified as:
Which is not true, so the area inside of the parabola should be shaded, resulting in the following graph: