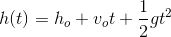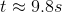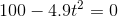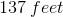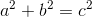Applications of Quadratic Equations
Help Questions
College Algebra › Applications of Quadratic Equations
Quadratic equations appear often in physics. The basic kinematic equations for the position 



This is a quadratic function in 

to express the "height" 




Find the time required for a ball dropped from a height of 100 m from rest to reach the ground using the quadratic function for height written below,
(Hint, what is the value of the height 
Explanation
We're given the function,
We know that the gravitational acceleration on earth is:

Because the ball starts at rest, the initial velocity 
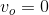
We are given the initial height,

When the ball reaches the ground, the height is "zero," so the value of 

(Note that although taking the square root of both sides of an equation will produce positive and negative solutions, we ignore the negative solution since "negative time" makes no sense in the context of this problem).
A sidewalk on a street corner reaches from a library to a bookstore making an L shape around that corner. The L shaped path has one length that is twice as long as the other. The diagonal path being built between the two buildings will be 102 feet long. How many feet shorter is the diagonal path than the traditional L shaped path around the corner?
The diagonal path would be longer.
Explanation
Use Pythagorean Theorem to solve.
Since the path around the corner is 3x, 3 times the