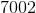Multiplication with Whole Numbers
Help Questions
Basic Math › Multiplication with Whole Numbers
Explanation

Start with 




Next, do 


Now, write down 





Now, do 




Next, do 

Finally, add these two numbers together.
Please choose the best answer for the question below.
What is
Explanation

Use a calculator to check your work if allowed, but if not, then I'd reccommend the following method, breaking the problem down into smaller pieces.
And then add your results:
Solve for 
Explanation
To solve this equation, follow order of operations:
First we do the calculations inside the parentheses.
Then we subtract to get our final answer.
What is
Explanation
You can simplify this problem:




What is the solution of the above equation?
Explanation
We can see this by implementing objects.


^ We can see that there are 21 objects.
Solve for 
Explanation
To solve for m we need to isolate m on one side of the equation and all other numbers on the other side of the equation.
Our first step is to divide by 12 on both sides. Remember to undo an operation from one side of the equation and cancel out a number we need to perform the opposite operation. If you have a number multiplied by another number or a variable you need to divide to cancel out that said number.
Then we divide by 3 to get our final answer.