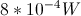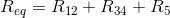Circuit Relationships
Help Questions
AP Physics C: Electricity and Magnetism › Circuit Relationships
A simple circuit contains two 
Explanation
The power supplied to the circuit can be calculated using the equation:
To use this equation, we need to find the equivalent resistance of the circuit. Use the equation for equivalent resistance in parallel:
Now that we have the resistance and the voltage, we can solve for the power.
A simple circuit contains two 
Explanation
The power supplied to the circuit can be calculated using the equation:
To use this equation, we need to find the equivalent resistance of the circuit. Use the equation for equivalent resistance in parallel:
Now that we have the resistance and the voltage, we can solve for the power.
A simple circuit consists of a 

Explanation
One of the formulas for power is 
Using these values, we can solve for power.
A simple circuit consists of a 

Explanation
One of the formulas for power is 
Using these values, we can solve for power.
A cicuit with a voltage source of 40V has a 
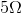


What is the current supplied by the source?
Explanation
The current supplied by the source can be calculated using a derivation of Ohm's law:
Start by finding the equivalent resistance of the circuit.
Sum the first two resistors in series:
Calculate the equivalent resistance of the two resistors in parallel:
Now, all of the reistances can be viewed as being in series.
Returning to our current calulation, we can find our final answer:
A cicuit with a voltage source of 40V has a 
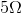


What is the current supplied by the source?
Explanation
The current supplied by the source can be calculated using a derivation of Ohm's law:
Start by finding the equivalent resistance of the circuit.
Sum the first two resistors in series:
Calculate the equivalent resistance of the two resistors in parallel:
Now, all of the reistances can be viewed as being in series.
Returning to our current calulation, we can find our final answer:

What is the current delivered to the curcuit by the battery?
Explanation
Using Ohm's law to solve for the value of the current from the battery requires calculation of the equivalent resistance of the circuit.
The resistors R2 and R3 are in parallel with one another. Once combined, their requivalent resistor (R23) is in series with R1.

The equivalent resistance is thus given by:
Use this value and the given voltage to solve for the current in the circuit:

What is the current delivered to the curcuit by the battery?
Explanation
Using Ohm's law to solve for the value of the current from the battery requires calculation of the equivalent resistance of the circuit.
The resistors R2 and R3 are in parallel with one another. Once combined, their requivalent resistor (R23) is in series with R1.

The equivalent resistance is thus given by:
Use this value and the given voltage to solve for the current in the circuit:
Three resistors R1, R2, and R3 and the capacitor, C, are connected to an ideal battery V to complete the circuit as shown.

After the circuit has been connected for a very long time, the currents in each branch of the circuit are measured to be some values 



Which of the following equations is a correct expression regarding the voltage of the circuit after a long time?
Explanation
Identifying the sum of the voltage drops and rises (Kirchoff's Loop Law) around the three possible loops of this circuit is the key to answering this question correctly. The following signs can be assigned to each of the circuit elements based on the direction of the currents given.
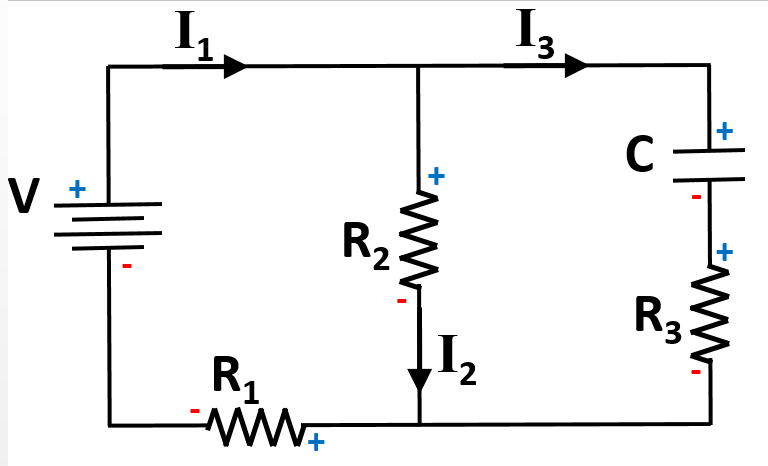
Use Ohm's law and the equation for capacitance to derive terms for the voltage across each element of the circuit.
There are three possible paths through the circuit, resulting in three correct equations that could be derived:
Only one of the given answer options matches up correctly to these.
Three resistors R1, R2, and R3 and the capacitor, C, are connected to an ideal battery V to complete the circuit as shown.

After the circuit has been connected for a very long time, the currents in each branch of the circuit are measured to be some values 



Which of the following equations is a correct expression regarding the voltage of the circuit after a long time?
Explanation
Identifying the sum of the voltage drops and rises (Kirchoff's Loop Law) around the three possible loops of this circuit is the key to answering this question correctly. The following signs can be assigned to each of the circuit elements based on the direction of the currents given.

Use Ohm's law and the equation for capacitance to derive terms for the voltage across each element of the circuit.
There are three possible paths through the circuit, resulting in three correct equations that could be derived:
Only one of the given answer options matches up correctly to these.