Motion

Help Questions

AP Physics 1 › Motion

Questions 1 - 10

A man throws a ball straight up in the air at a velocity of $20\frac{m}{s}$ . If there is a constant air resistance force of against the motion of the ball, what is the maximum height of the ball?

Explanation

We first need to find the net force acting on the ball during flight. We can then use the net force and Newton's second law to find the total acceleration on the ball.

$F_{net}=F_g+F_{air}$

$F_{net}=mg+F_{air}$

$F_{net}=(2kg)(-9.8\frac{m}{s^2})+0.4N$

$F_{net}=-19.2N$

Use this net force to find the acceleration.

$F_{net}=ma$

$a=-9.6\frac{m}{s^2}$

From here, there are two ways to solve. One way uses kinematic equations, and the other uses energy. We will solve using energy.

Total energy must be conserved during the throw, so the initial kinetic energy must equal the final potential energy (since velocity is zero at the maximum height).

$\frac{1}{2}mv_i^2+mgh_i=\frac{1}{2}mv_f^2+mgh_f$

$\frac{1}{2}mv_i^2+mg(0m)=\frac{1}{2}m(0\frac{m}{s})^2+mgh_f$

$\frac{1}{2}mv_i^2=mgh_f$

Use the given initial velocity to find the final height.

$\frac{1}{2}(2kg)(20\frac{m}{s})^2=(2kg)(9.6\frac{m}{s^2})(h)$

$h=\frac{\frac{1}{2}(2kg)(20\frac{m}{s})^2}{(2kg)(9.6\frac{m}{s^2})}$

A car of mass is initially at rest, and then accelerates at $2.0 \frac{m}{s^2}$ for . What is the kinetic energy of the car at time ?

Explanation

The first step will be to find the final velocity of the car. We know the acceleration and time, so we can find the final velocity using kinematics. The initial velocity is zero, since the car starts at rest.

$v=(0\frac{m}{s})+(2\frac{m}{s^2})(14s)=28\frac{m}{s}$

Use this velocity and the mass of the car to solve for the final kinetic energy.

$KE=\frac{1}{2}mv^2$

$KE=\frac{1}{2}(1000kg)(28\frac{m}{s})^2$

A man throws a ball straight up in the air at a velocity of $20\frac{m}{s}$ . If there is a constant air resistance force of against the motion of the ball, what is the maximum height of the ball?

Explanation

We first need to find the net force acting on the ball during flight. We can then use the net force and Newton's second law to find the total acceleration on the ball.

$F_{net}=F_g+F_{air}$

$F_{net}=mg+F_{air}$

$F_{net}=(2kg)(-9.8\frac{m}{s^2})+0.4N$

$F_{net}=-19.2N$

Use this net force to find the acceleration.

$F_{net}=ma$

$a=-9.6\frac{m}{s^2}$

From here, there are two ways to solve. One way uses kinematic equations, and the other uses energy. We will solve using energy.

Total energy must be conserved during the throw, so the initial kinetic energy must equal the final potential energy (since velocity is zero at the maximum height).

$\frac{1}{2}mv_i^2+mgh_i=\frac{1}{2}mv_f^2+mgh_f$

$\frac{1}{2}mv_i^2+mg(0m)=\frac{1}{2}m(0\frac{m}{s})^2+mgh_f$

$\frac{1}{2}mv_i^2=mgh_f$

Use the given initial velocity to find the final height.

$\frac{1}{2}(2kg)(20\frac{m}{s})^2=(2kg)(9.6\frac{m}{s^2})(h)$

$h=\frac{\frac{1}{2}(2kg)(20\frac{m}{s})^2}{(2kg)(9.6\frac{m}{s^2})}$

A man throws a ball straight up in the air at a velocity of $20\frac{m}{s}$ . If there is a constant air resistance force of against the motion of the ball, what is the maximum height of the ball?

Explanation

We first need to find the net force acting on the ball during flight. We can then use the net force and Newton's second law to find the total acceleration on the ball.

$F_{net}=F_g+F_{air}$

$F_{net}=mg+F_{air}$

$F_{net}=(2kg)(-9.8\frac{m}{s^2})+0.4N$

$F_{net}=-19.2N$

Use this net force to find the acceleration.

$F_{net}=ma$

$a=-9.6\frac{m}{s^2}$

From here, there are two ways to solve. One way uses kinematic equations, and the other uses energy. We will solve using energy.

Total energy must be conserved during the throw, so the initial kinetic energy must equal the final potential energy (since velocity is zero at the maximum height).

$\frac{1}{2}mv_i^2+mgh_i=\frac{1}{2}mv_f^2+mgh_f$

$\frac{1}{2}mv_i^2+mg(0m)=\frac{1}{2}m(0\frac{m}{s})^2+mgh_f$

$\frac{1}{2}mv_i^2=mgh_f$

Use the given initial velocity to find the final height.

$\frac{1}{2}(2kg)(20\frac{m}{s})^2=(2kg)(9.6\frac{m}{s^2})(h)$

$h=\frac{\frac{1}{2}(2kg)(20\frac{m}{s})^2}{(2kg)(9.6\frac{m}{s^2})}$

A car of mass is initially at rest, and then accelerates at $2.0 \frac{m}{s^2}$ for . What is the kinetic energy of the car at time ?

Explanation

$v=(0\frac{m}{s})+(2\frac{m}{s^2})(14s)=28\frac{m}{s}$

Use this velocity and the mass of the car to solve for the final kinetic energy.

$KE=\frac{1}{2}mv^2$

$KE=\frac{1}{2}(1000kg)(28\frac{m}{s})^2$

A car of mass is initially at rest, and then accelerates at $2.0 \frac{m}{s^2}$ for . What is the kinetic energy of the car at time ?

Explanation

$v=(0\frac{m}{s})+(2\frac{m}{s^2})(14s)=28\frac{m}{s}$

Use this velocity and the mass of the car to solve for the final kinetic energy.

$KE=\frac{1}{2}mv^2$

$KE=\frac{1}{2}(1000kg)(28\frac{m}{s})^2$

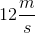
A ball is thrown at a velocity of $12\frac{m}{s}$ at an angle of from the horizontal. What are the ball's horizontal and vertical velocities?

Ball_32_degrees

$v_y=6.36\frac{m}{s}\ \textup{and}\ v_x=10.18\frac{m}{s}$

$v_y=10.18\frac{m}{s}\ \textup{and}\ v_x=6.36\frac{m}{s}$

$v_y=1.26\frac{m}{s}\ \textup{and}\ v_x=3.97\frac{m}{s}$

$v_y=3.97\frac{m}{s}\ \textup{and}\ v_x=1.26\frac{m}{s}$

There is not enough information to solve this problem

Explanation

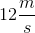
The velocity of $12\frac{m}{s}$ can be broken into horizontal and vertical components by using trigonometry. Think of the figure below, where x and y velocity components of the total velocity are shown.

Ball_32_degrees_xy

Use the total velocity, the x-component, and the y-component to form a right triangle below.

Xy_velocities

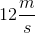
Treating $12\frac{m}{s}$ as the hypotenuse, x-component as the leg adjacent, and y-component as the leg opposite, you can conclude that the velocities are related through trigonometric identities.

$v_y=v\sin\theta$

$v_x=v\cos\theta$

Plugging in the given values, we can solve for the x and y velocity components.

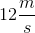
$v_y=(12\frac{m}{s})\sin(32^o)=6.36\frac{m}{s}$

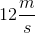
$v_x=(12\frac{m}{s})\cos(32^o)=10.18\frac{m}{s}$

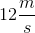
A ball is thrown at a velocity of $12\frac{m}{s}$ at an angle of from the horizontal. What are the ball's horizontal and vertical velocities?

Ball_32_degrees

$v_y=6.36\frac{m}{s}\ \textup{and}\ v_x=10.18\frac{m}{s}$

$v_y=10.18\frac{m}{s}\ \textup{and}\ v_x=6.36\frac{m}{s}$

$v_y=1.26\frac{m}{s}\ \textup{and}\ v_x=3.97\frac{m}{s}$

$v_y=3.97\frac{m}{s}\ \textup{and}\ v_x=1.26\frac{m}{s}$

There is not enough information to solve this problem

Explanation

Ball_32_degrees_xy

Use the total velocity, the x-component, and the y-component to form a right triangle below.

Xy_velocities

Treating $12\frac{m}{s}$ as the hypotenuse, x-component as the leg adjacent, and y-component as the leg opposite, you can conclude that the velocities are related through trigonometric identities.

$v_y=v\sin\theta$

$v_x=v\cos\theta$

Plugging in the given values, we can solve for the x and y velocity components.

$v_y=(12\frac{m}{s})\sin(32^o)=6.36\frac{m}{s}$

$v_x=(12\frac{m}{s})\cos(32^o)=10.18\frac{m}{s}$

A ball is thrown at a velocity of $12\frac{m}{s}$ at an angle of from the horizontal. What are the ball's horizontal and vertical velocities?

Ball_32_degrees

$v_y=6.36\frac{m}{s}\ \textup{and}\ v_x=10.18\frac{m}{s}$

$v_y=10.18\frac{m}{s}\ \textup{and}\ v_x=6.36\frac{m}{s}$

$v_y=1.26\frac{m}{s}\ \textup{and}\ v_x=3.97\frac{m}{s}$

$v_y=3.97\frac{m}{s}\ \textup{and}\ v_x=1.26\frac{m}{s}$

There is not enough information to solve this problem

Explanation

Ball_32_degrees_xy

Use the total velocity, the x-component, and the y-component to form a right triangle below.

Xy_velocities

Treating $12\frac{m}{s}$ as the hypotenuse, x-component as the leg adjacent, and y-component as the leg opposite, you can conclude that the velocities are related through trigonometric identities.

$v_y=v\sin\theta$

$v_x=v\cos\theta$

Plugging in the given values, we can solve for the x and y velocity components.

$v_y=(12\frac{m}{s})\sin(32^o)=6.36\frac{m}{s}$

$v_x=(12\frac{m}{s})\cos(32^o)=10.18\frac{m}{s}$

Pully_system

What is the acceleration of the system shown above? (Assume the table is frictionless and the mass of the rope connecting blocks is negligible).

$1.8\frac{m}{s^2}$

$14.0\frac{m}{s^2}$

$2.2\frac{m}{s^2}$

$10\frac{m}{s^2}$

$7.2\frac{m}{s^2}$

Explanation

The force that translates to the entire system is that of gravity acting on the mass hanging over the ledge.

$F = mg = 14kg(10m/s^{2}) = 140 N$

140N is the total force acting on the system, which has a mass equal to both blocks combined (65 kg + 14 kg = 79 kg). We can find the acceleration using Newton's second law.

$a = \frac{F}{m}$

$a = \frac{140 N}{79 kg} = 1.8 m/s^{2}$

Page 1 of 11

Return to subject

AI TutorYour personal study buddy

Question of the DayDaily practice to build your skills

FlashcardsStudy and memorize key concepts

WorksheetsBuild custom practice quizzes

AI SolverStep-by-step problem solutions

Learn by ConceptMaster concepts step by step

Diagnostic TestsAssess your knowledge level

Practice TestsTest your skills with exam questions

GamesLearn through free games