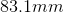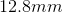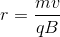Magnetic Force
Help Questions
AP Physics 2 › Magnetic Force
A proton is traveling parallel to a wire in the same direction as the conventional current. The proton is traveling at 


None of these
Explanation
Finding the magnetic field at the location of the proton.
Converting 

Using
A circuit contains a 


None of these
Explanation
Since the electron is stationary, there will be no magnetic force, as magnetic force requires the particle to be both charged and to be moving.
What is the force experienced by a 



There is no net force on the charge
Explanation
To find the force experienced by the charge, we use this equation:
Because the charge is moving at an angle from perpendicular, we need to take the cross product into account.
Theta is the angle from perpendicular, which is 
A proton traveling at 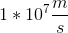


The proton’s mass is 

Explanation

A charged particle moving through a perpendicular magnetic field feels a Lorentz force equal to the formula:



We can set these two equations equal to one another, allowing us to solve for the radius of the arc.
Once the particle travels through a semicircle, it is laterally one diameter in distance from where is started (i.e. twice the radius of the circle).
Twice this value is the lateral offset of its crash point from the entrance:
A circuit contains a 


None of these
Explanation
Magnetic fields do not affect charges that are moving parallel to them.
Thus, the magnetic force will be at a maximum when moving perpendicular to the field, and at zero when moving parallel to the field.
A particle with a charge of 


There is no force on the particle
Explanation
The equation for finding the force on a moving charged particle in a magnetic field is as follows:
Here, 




Another way to write the equation without the cross-product is as follows:
Here, 
For our problem, because theta is 

Therefore, the force on the particle is 0.3N.
A charged particle, Q, is traveling along a magnetic field, B, with speed v. What is the magnitude of the force the particle experiences?
Zero
Explanation
Charged particles only experience a magnetic force when some component of their velocity is perpendicular to the magnetic field. Here, the velocity is parallel to the magnetic field so the particle does not experience a force.
An 


There is no force on the charge
Explanation
The equation for force on a charge moving through a magnetic field is:
Because the velocity is perpendicular to the field, the cross product doesn't matter, and we can do simple multiplication.
Therefore, the force on the charge is
Two electrons are traveling parallel to each other 
None of these
Explanation
Using
Where









Combining equations:
Solving for
Plugging in values:
If a 10C charged particle is traveling perpendicularly to a magnetic field of 5T at a speed of 
Explanation
This question is presenting us with a scenario in which a charged particle is traveling with a certain velocity through a magnetic field. In this situation, we're being asked to determine what the force experienced by this particle is.
To solve this question, we'll need to determine what kind of force this particle is likely to experience. Since we're told that the particle is traveling in a magnetic field, it would make sense that this particle is going to be affected by a magnetic force. Thus, we'll need to use the equation for magnetic force.
Moreover, since we're told in the question stem that this particle is traveling perpendicularly to the magnetic field, we know that 

Now, all we need to do is plug in the values given to us in order to calculate the resulting force.