Quartiles
Help Questions
Algebra II › Quartiles
Determine the interquartile range of the following numbers:
42, 51, 62, 47, 38, 50, 54, 43
None of these
Explanation
How do you find the interquartile range?
We can find the interquartile range or IQR in four simple steps:
- Order the data from least to greatest
- Find the median
- Calculate the median of both the lower and upper half of the data
- The IQR is the difference between the upper and lower medians
Step 1: Order the data
In order to calculate the IQR, we need to begin by ordering the values of the data set from the least to the greatest. Likewise, in order to calculate the median, we need to arrange the numbers in ascending order (i.e. from the least to the greatest).
Let's sort an example data set with an odd number of values into ascending order.
Now, let's perform this task with another example data set that is comprised of an even number of values.
Rearrange into ascending order.
Step 2: Calculate the median
Next, we need to calculate the median. The median is the "center" of the data. If the data set has an odd number of data points, then the mean is the centermost number. On the other hand, if the data set has an even number of values, then we will need to take the arithmetic average of the two centermost values. We will calculate this average by adding the two numbers together and then dividing that number by two.
First, we will find the median of a set with an odd number of values. Cross out values until you find the centermost point
The median of the odd valued data set is four.
Now, let's find the mean of the data set with an even number of values. Cross out values until you find the two centermost points and then calculate the average the two values.
Find the average of the two centermost values.
The median of the even valued set is four.
Step 3: Upper and lower medians
Once we have found the median of the entire set, we can find the medians of the upper and lower portions of the data. If the data set has an odd number of values, we will omit the median or centermost value of the set. Afterwards, we will find the individual medians for the upper and lower portions of the data.
Omit the centermost value.
Find the median of the lower portion.
Calculate the average of the two values.
The median of the lower portion is
Find the median of the upper portion.
Calculate the average of the two values.
The median of the upper potion is
If the data set has an even number of values, we will use the two values used to calculate the original median to divide the data set. These values are not omitted and become the largest value of the lower data set and the lowest values of the upper data set, respectively. Afterwards, we will calculate the medians of both the upper and lower portions.
Find the median of the lower portion.
The median of the lower portion is two.
Find the median of the upper portion.
The median of the upper portion is eight.
Step 4: Calculate the difference
Last, we need to calculate the difference of the upper and lower medians by subtracting the lower median from the upper median. This value equals the IQR.
Let's find the IQR of the odd data set.
Finally, we will find the IQR of the even data set.
In order to better illustrate these values, their positions in a box plot have been labeled in the provided image.
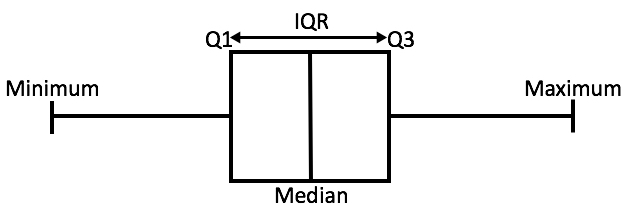
Now that we have solved a few examples, let's use this knowledge to solve the given problem.
Solution:
First reorder the numbers in ascending order:
38, 42, 43, 47, 50, 51, 54, 62
Then divide the numbers into 2 groups, each containing an equal number of values:
(38, 42, 43, 47)(50, 51, 54, 62)
Q1 is the median of the group on the left, and Q3 is the median of the group on the right. Because there is an even number in each group, we'll need to find the average of the 2 middle numbers:
The interquartile range is the difference between Q3 and Q1:
Give the interquartile range of a data set with the following characteristics.
Mean: 72.1
Median: 70
Standard deviation: 4.6
It cannot be determined from the information given.
Explanation
The interquartile range is the difference between the first and third quartiles. The two pieces of information needed to determine interquartile range, the first and third quartiles, are missing; therefore, it is impossible to answer the question without more information.
Given the following set of data, what is twice the interquartile range?
Explanation
How do you find the interquartile range?
We can find the interquartile range or IQR in four simple steps:
- Order the data from least to greatest
- Find the median
- Calculate the median of both the lower and upper half of the data
- The IQR is the difference between the upper and lower medians
Step 1: Order the data
In order to calculate the IQR, we need to begin by ordering the values of the data set from the least to the greatest. Likewise, in order to calculate the median, we need to arrange the numbers in ascending order (i.e. from the least to the greatest).
Let's sort an example data set with an odd number of values into ascending order.
Now, let's perform this task with another example data set that is comprised of an even number of values.
Rearrange into ascending order.
Step 2: Calculate the median
Next, we need to calculate the median. The median is the "center" of the data. If the data set has an odd number of data points, then the mean is the centermost number. On the other hand, if the data set has an even number of values, then we will need to take the arithmetic average of the two centermost values. We will calculate this average by adding the two numbers together and then dividing that number by two.
First, we will find the median of a set with an odd number of values. Cross out values until you find the centermost point
The median of the odd valued data set is four.
Now, let's find the mean of the data set with an even number of values. Cross out values until you find the two centermost points and then calculate the average the two values.
Find the average of the two centermost values.
The median of the even valued set is four.
Step 3: Upper and lower medians
Once we have found the median of the entire set, we can find the medians of the upper and lower portions of the data. If the data set has an odd number of values, we will omit the median or centermost value of the set. Afterwards, we will find the individual medians for the upper and lower portions of the data.
Omit the centermost value.
Find the median of the lower portion.
Calculate the average of the two values.
The median of the lower portion is
Find the median of the upper portion.
Calculate the average of the two values.
The median of the upper potion is
If the data set has an even number of values, we will use the two values used to calculate the original median to divide the data set. These values are not omitted and become the largest value of the lower data set and the lowest values of the upper data set, respectively. Afterwards, we will calculate the medians of both the upper and lower portions.
Find the median of the lower portion.
The median of the lower portion is two.
Find the median of the upper portion.
The median of the upper portion is eight.
Step 4: Calculate the difference
Last, we need to calculate the difference of the upper and lower medians by subtracting the lower median from the upper median. This value equals the IQR.
Let's find the IQR of the odd data set.
Finally, we will find the IQR of the even data set.
In order to better illustrate these values, their positions in a box plot have been labeled in the provided image.

Now that we have solved a few examples, let's use this knowledge to solve the given problem.
Solution:
First, we need to put the data in order from smallest to largest.






The median of the lower half falls between two values.
The median of the upper half falls between two values.
The interquartile range is the difference between the third and first quartiles.
Multiply by 
Determine the first quartile and third quartile from the following list:
Explanation
To find the first and third quartile of the data set we first need to find the median of the data set. The median is the middle entry of the data set when entries are in ascending order therefore, the median is 10.
To find the first quartile, we need to break our data set into a subset that is between the first entry and the median. This set is:
Because the first quartile is the median of this subset we get the first quartile to equal 3.
The third quartile is found by taking the subset that is the median to the last entry of the data set. This subset is:
Because the third quartile is the median of the new subset we get the third quartile to equal 25.
Identify the first and third quartiles for the following set of numbers.
{11, 14, 9, 2, 27, 26, 5, 8, 19, 10, 12, 6}
Explanation
{11, 14, 9, 2, 27, 26, 5, 8, 19, 10, 12, 6}
First, arrange the values in numerical order.
{2, 5, 6, 8, 9, 10, 11, 12, 14, 19, 26, 27}
Quartiles are the values that divide a set into four equal parts. Since this set has twelve values, "cut" the data after the 3rd and 9th value to find the 1st and 3rd quartile, respectively.
{2, 5, 6,| 8, 9, 10, 11, 12, 14,| 19, 26, 27}
The quartile will be the average of the values on either side of the "cut."
First Quartile = (6+8)/2=7
Third Quartile = (14+19)/2=16.5
Salespeople who land in the top quartile of average customer satisfaction ratings at the end of the year receive a bonus. Among the set of average ratings below, what is the cutoff for receiving the bonus?
{98, 55, 67, 88, 85, 91, 83, 65, 77, 83}
Explanation
{98, 55, 67, 88, 85, 91, 83, 65, 77, 83}
Rearrange the values in order.
{55, 65, 67, 77, 83, 83, 85, 88, 91, 98}
To get quartiles, "cut" the data into four.
{55, 65, 6**|7, 77, 83,|** 83, 85, 8**|**8, 91, 98}
As you can see, the third "cut" is right at 88. Which means 88 is the cutoff for the top quartile based on this set of data.
In the above data set, which of the following represents the 3rd Quartile (Upper Quartile)?
Impossible to determine for this data set.
Explanation
The Upper Quartile of the data set is the median value of the upper half of the values; to solve for the upper quartile, the first step is to put the data in sequential order:
Becomes:

There are 6 values in the upper half of our data, so the median of the bolded values, the upper quartile, is halfway between the third and fourth values. Since both values are 14, the median of the upper half of our data set, the upper quartile, is 14.
Find the first quartile of the following data set:
Explanation
Find the first quartile of the following data set:
Begin by finding the median:
To find the median, we should first put our numbers in increasing order:
Next, the median will simply be the number in the middle.
We have 11 terms, so our median will be the 6th term in the sequence:
So 54 is our median
The first quartile is sort of like the median of the first half of our data set. It is the term that is one quarter of the way through:
So in this case, our first quartile is 23, because it is the term one-quarter of the way into our data set.
Find the third quartile of the following data set:
Explanation
Find the third quartile of the following data set:
Begin by finding the median:
To find the median, we should first put our numbers in increasing order:
Next, the median will simply be the number in the middle.
We have 11 terms, so our median will be the 6th term in the sequence:
So 54 is our median
The third quartile is sort of like the median of the second half of our data set. It is the term that is three quarters of the way through:
So our third quartile is 117
In the following set of data, which number represents 
Explanation
Reorder the data set in chronological order from least to greatest.
The first quartile 

The second quartile 

The third quartile 

The answer is:





















































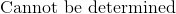






































![[2,1,8,4,3,5,7]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/736080/gif.latex)





![[2,1,8,4,3,5,7]\rightarrow[1,2,3,4,5,7,8]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/736081/gif.latex)
