Absolute Value
Help Questions
Algebra II › Absolute Value
Solve for 
Explanation
To solve absolute value equations, we must understand that the absoute value function makes a value positive. So when we are solving these problems, we must consider two scenarios, one where the value is positive and one where the value is negative.
and
This gives us:

However, this question has an 




Our final solution is then
Solve for 
Explanation
To solve absolute value equations, we must understand that the absoute value function makes a value positive. So when we are solving these problems, we must consider two scenarios, one where the value is positive and one where the value is negative.
and
This gives us:

However, this question has an 




Our final solution is then
Solve the absolute value equation:
Explanation
Recall that the absolute value sign will convert any value to a positive sign. There will be no occurrences of 
There are no solutions for this equation.
The answer is:
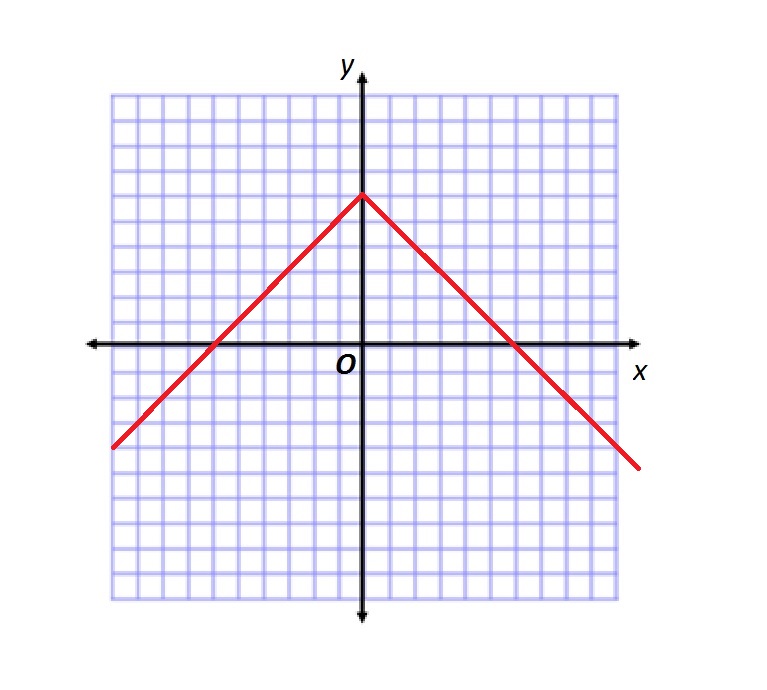
Refer to the above figure.
Which of the following functions is graphed?
Explanation
Below is the graph of 

The given graph is the graph of 



The function graphed is therefore
Give the vertex of the graph of the function 
None of the other choices gives the correct response.
Explanation
Let
The graph of this basic absolute value function is a "V"-shaped graph with a vertex at the origin, or the point with coordinates 


or, alternatively written,
The graph of 






Refer to the above figure.
Which of the following functions is graphed?
Explanation
Below is the graph of 

The given graph is the graph of 



The function graphed is therefore
Give the vertex of the graph of the function 
None of the other choices gives the correct response.
Explanation
Let
The graph of this basic absolute value function is a "V"-shaped graph with a vertex at the origin, or the point with coordinates 


or, alternatively written,
The graph of 





Solve the absolute value equation:
Explanation
Recall that the absolute value sign will convert any value to a positive sign. There will be no occurrences of 
There are no solutions for this equation.
The answer is:
Solve:
Explanation
Separate the absolute value and solve both the positive and negative components of the absolute value.
Solve the first equation. Add 
Add two on both sides.
Divide by five on both sides.
One of the solutions is 
Evaluate the second equation. Distribute the negative sign in the binomial.
Subtract 
Add two on both sides.
If we substitute this value back to the original equation, the equation becomes invalid.
The answer is:
Solve:
Explanation
Separate the absolute value and solve both the positive and negative components of the absolute value.
Solve the first equation. Add 
Add two on both sides.
Divide by five on both sides.
One of the solutions is 
Evaluate the second equation. Distribute the negative sign in the binomial.
Subtract 
Add two on both sides.
If we substitute this value back to the original equation, the equation becomes invalid.
The answer is:


















































