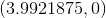Graphing Exponential Functions
Help Questions
Algebra II › Graphing Exponential Functions
Determine whether each function represents exponential decay or growth.
a) decay
b) growth
a) growth
b) growth
a) decay
b) decay
a) growth
b) decay
Explanation
a)
This is exponential decay since the base, 


b)
This is exponential growth since the base, 

Match each function with its graph.
1.
2.
3.
a.
b.
c.
1.
2.
3.
1.
2.
3.
1.
2.
3.
1.
2.
3.
Explanation
For 





For 



For 



What is the 

Explanation
The 



Thus, to find the 

In this case, you will get,

In 2010, the population of trout in a lake was 416. It has increased to 521 in 2015.
Write an exponential function of the form 

Explanation
We need to determine the constants 




To get 



Using a calculator, 

Then our model equation for the fish population is
What is the 

Explanation
The 

Substituting this in to our funciton, we get:
What is the 

There is no 
Explanation
The 


Thus, to find the 


Thus, we get:
Which of the following correctly describes the graph of an exponential function with a base of three?
It starts out by gradually increasing and then increases faster and faster.
It starts by increasing quickly and then levels out.
It begins by decreasing quickly and then levels out.
It begins by decreasing gradually and then decreases more quickly.
It stays constant.
Explanation
Exponential functions with a base greater than one are models of exponential growth. Thus, we know that our function will increase and not decrease. Remembering the graph of an exponential function, we can determine that the graph will begin gradually, almost like a flat line. Then, as 

An exponential funtion 







Explanation
To determine the constant 







To find 








We can write our equation as 


Then 
Our model equation is 
Give the 

The graph has no 
Explanation
Set 
We need not work further. It is impossible to raise a positive number 2 to any real power to obtain a negative number. Therefore, the equation has no solution, and the graph of 

What is/are the asymptote(s) of the graph of the function 

Explanation
An exponential function of the form
has as its one and only asymptote the horizontal line 
Since we define 

then 
and the only asymptote is the line of the equation