Tetrahedrons
Help Questions
ACT Math › Tetrahedrons
A regular tetrahedron has a surface area of 

Explanation
A regular tetrahedron has 4 triangular faces. The area of one of these faces is given by:
Because the surface area is the area of all 4 faces combined, in order to find the area for one of the faces only, we must divide the surface area by 4. We know that the surface area is 
Since we now have the area of one face, and we know the height of one face is 
Therefore, the length of the base of one face is 
A regular tetrahedron has a surface area of 

Explanation
A regular tetrahedron has 4 triangular faces. The area of one of these faces is given by:
Because the surface area is the area of all 4 faces combined, in order to find the area for one of the faces only, we must divide the surface area by 4. We know that the surface area is 
Since we now have the area of one face, and we know the height of one face is 
Therefore, the length of the base of one face is 
Calculate the diagonal of a regular tetrahedron (all of the faces are equilateral triangles) with side length 
Explanation
The diagonal of a shape is simply the length from a vertex to the center of the face or vertex opposite to it. With a regular tetrahedron, we have a face opposite to the vertex, and this basically amounts to calculating the height of our shape.
We know that the height of a tetrahedron is 

which gives us the correct answer.
What is the surface area of a regular tetrahedron when its volume is 27?
Explanation
The problem is essentially asking us to go from a three-dimensional measurement to a two-dimensional one. In order to approach the problem, it's helpful to see how volume and surface area are related.
This can be done by comparing the formulas for surface area and volume:
We can see that both calculation revolve around the edge length.
That means, if we can solve for 
Now that we know 
Calculate the diagonal of a regular tetrahedron (all of the faces are equilateral triangles) with side length 
Explanation
The diagonal of a shape is simply the length from a vertex to the center of the face or vertex opposite to it. With a regular tetrahedron, we have a face opposite to the vertex, and this basically amounts to calculating the height of our shape.
We know that the height of a tetrahedron is 

which gives us the correct answer.
What is the surface area of a regular tetrahedron when its volume is 27?
Explanation
The problem is essentially asking us to go from a three-dimensional measurement to a two-dimensional one. In order to approach the problem, it's helpful to see how volume and surface area are related.
This can be done by comparing the formulas for surface area and volume:
We can see that both calculation revolve around the edge length.
That means, if we can solve for 
Now that we know 
What is the surface area of a regular tetrahedron with a slant height of 
Cannot be determined
Explanation
If this is a regular tetrahedron, then all four triangles are equilateral triangles.
If the slant height is 

In order to solve for the surface area, we can use the formula
where 
The problem has not given the edge; however, it has provided information that will allow us to solve for the edge and therefore the surface area.
Picture an equilateral triangle with a height 
Drawing in the height will divide the equilateral triangle into two 30/60/90 right triangles. Because this is an equilateral triangle, we can deduce that finding the measure of the hypotenuse will suffice to solve for the edge length (
In order to solve for the hypotenuse of one of the right triangles, either trig functions or the rules of the special 30/60/90 triangle can be used.
Using trig functions, one option is using 
Rearranging the equation to solve for 
Now that 
What is the surface area of a regular tetrahedron with a slant height of 
Cannot be determined
Explanation
If this is a regular tetrahedron, then all four triangles are equilateral triangles.
If the slant height is 

In order to solve for the surface area, we can use the formula
where 
The problem has not given the edge; however, it has provided information that will allow us to solve for the edge and therefore the surface area.
Picture an equilateral triangle with a height 
Drawing in the height will divide the equilateral triangle into two 30/60/90 right triangles. Because this is an equilateral triangle, we can deduce that finding the measure of the hypotenuse will suffice to solve for the edge length (
In order to solve for the hypotenuse of one of the right triangles, either trig functions or the rules of the special 30/60/90 triangle can be used.
Using trig functions, one option is using 
Rearranging the equation to solve for 
Now that 
What is the length of an edge of a regular tetrahedron if its surface area is 156?
Explanation
The only given information is the surface area of the regular tetrahedron.
This is a quick problem that can be easily solved for by using the formula for the surface area of a tetrahedron:
If we substitute in the given infomation, we are left with the edge being the only unknown.
What is the length of an edge of a regular tetrahedron if its surface area is 156?
Explanation
The only given information is the surface area of the regular tetrahedron.
This is a quick problem that can be easily solved for by using the formula for the surface area of a tetrahedron:
If we substitute in the given infomation, we are left with the edge being the only unknown.
















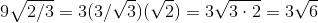









![\sqrt[3]{27 \cdot 6\sqrt{2}}=a](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/376629/gif.latex)

























