Parallelograms
Help Questions
ACT Math › Parallelograms

Note: Figure NOT drawn to scale.
Give the perimeter of Parallelogram 
Explanation
By the 45-45-90 Theorem, the lengths of the legs of 
Its hypotenuse has measure 
The perimeter of the parallelogram is

Note: Figure NOT drawn to scale.
To the nearest tenth, give the perimeter of Parallelogram 
Explanation
The perimeter of the parallelogram is

Note: Figure NOT drawn to scale.
Give the perimeter of Parallelogram 
Explanation
By the 45-45-90 Theorem, the lengths of the legs of 
Its hypotenuse has measure 
The perimeter of the parallelogram is



There is insufficient information to solve the problem.
Explanation





Note: Figure NOT drawn to scale.
To the nearest tenth, give the perimeter of Parallelogram 
Explanation
The perimeter of the parallelogram is



There is insufficient information to solve the problem.
Explanation





Parallelogram 



There is insufficient information to solve the problem.
Explanation
The area of a parallelogram is given by:
In this problem, the height is given as 




Parallelogram 



There is insufficient information to solve the problem.
Explanation
The area of a parallelogram is given by:
In this problem, the height is given as 



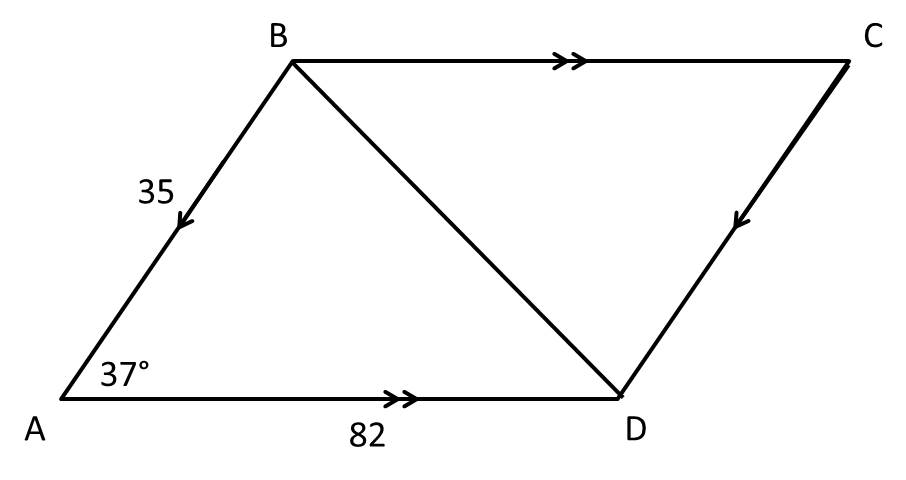


Explanation
To find the length of the diagonal, we can consider only the triangle 
The Law of Cosines:
Where 





From the problem:



Explanation
To find the length of the diagonal, we can consider only the triangle 
The Law of Cosines:
Where 





From the problem:
















































