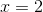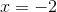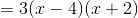How to factor the quadratic equation
Help Questions
ACT Math › How to factor the quadratic equation
Which of the following is a root of the function 
Explanation
The roots of a function are the x intercepts of the function. Whenever a function passes through a point on the x-axis, the value of the function is zero. In other words, to find the roots of a function, we must set the function equal to zero and solve for the possible values of x.

This is a quadratic trinomial. Let's see if we can factor it. (We could use the quadratic formula, but it's easier to factor when we can.)
Because the coefficient in front of the 
We will then group the first two terms and the last two terms.
We will next factor out a 2_x_ from the first two terms.
Thus, when factored, the original equation becomes (2_x_ + 1)(x – 4) = 0.
We now set each factor equal to zero and solve for x.
Subtract 1 from both sides.
2_x_ = –1
Divide both sides by 2.
Now, we set x – 4 equal to 0.
x – 4 = 0
Add 4 to both sides.
x = 4
The roots of f(x) occur where x = 
The answer is therefore 
What is the sum of all the values of 
Explanation
With quadratic equations, always begin by getting it into standard form:
Therefore, take our equation:
And rewrite it as:
You could use the quadratic formula to solve this problem. However, it is possible to factor this if you are careful. Factored, the equation can be rewritten as:
Now, either one of the groups on the left could be 


OR
The sum of these values is:
Which of the following values of 

Explanation
1. Factor the above equation:
2. Solve for 
and...
If x2 + x – 6 = 0, what does x equal?
2, –3
–2, 3
0, 6
6, 36
0, –6
Explanation
There are two ways to solve this problem. One option is to use the quadratic formula:

In this problem, a = 1, b = 1, and c = –6. However, there is a lot of room for computational error using this method.
Another option is to factor the equation using the reverse FOIL method. Because we have x2, we know that both factors must include x. Thus, so far we have (x )(x ). We also know that one factor must be negative and one must be positive if our last value (the L in FOIL) is to be negative. Thus, we have (x– ) (x+ ). The factors of 6 are 1, 2, 3, and 6, so our last values must multiply together to make 6. Therefore, our options are (x – 1)(x + 6), (x – 6)(x + 1), (x – 2)(x + 3), and (x – 3)(x + 2). However, because we need our middle value to be 1, the combination of the outer and inner values (O and I in FOIL), must add up to positive 1. Since only a combination of +/–2 and +/–3 can add to 1, we can eliminate our first two options. Then, because we need the positive value to be larger than the negative value, we can determine that the correct factorization is (x – 2)(x + 3). When we set each of these pieces equal to zero, we get x – 2 = 0 and x + 3 = 0. Thus, X equals 2 and –3. We can check our work using FOIL.
What are the two solutions to the following quadratic equation?


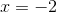


Explanation
The equation can be factored.
First pull out a common factor of three from each term.

Now, find the factors of the constant term that when added together result in the middle term.
The roots are what values will make the equation equal 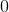
Therefore, the answers are 
x_2 + 3_x + 2 = 0
What are the values of x that are solutions to the equation?
–1, –1
–2, 0
–1, –2
0, 1
1, –2
Explanation
You factor the equation and get:
(x + 2)(x + 1) = 0
Then, you get x = –2 and x = –1.
Solve: x2+6x+9=0
3
6
9
12
-3
Explanation
Given a quadratic equation equal to zero you can factor the equation and set each factor equal to zero. To factor you have to find two numbers that multiply to make 9 and add to make 6. The number is 3. So the factored form of the problem is (x+3)(x+3)=0. This statement is true only when x+3=0. Solving for x gives x=-3. Since this problem is multiple choice, you could also plug the given answers into the equation to see which one works.
36x2 -12x - 15 = 0
Solve for x
-1/2 and 5/6
1/2 and 5/6
-1/2 and -5/6
1/2 and -1/3
1/2 and 1/3
Explanation
36x2 - 12x - 15 = 0
Factor the equation:
(6x + 3)(6x - 5) = 0
Set each side equal to zero
6x + 3 = 0
x = -3/6 = -1/2
6x – 5 = 0
x = 5/6
Find the roots of the equation 
Explanation
To factor this, we need to find a pair of numbers that multiplies to 6 and sums to 5. The numbers 2 and 3 work. (2 * 3 = 6 and 2 + 3 = 5)
(x + 2)(x + 3) = 0
x = –2 or x = –3
In the equation 

None of the other answers
Explanation
To solve, begin by factoring the equation. We know that in our two factors, one will begin with 





(If you are unsure, double check by expanding the equation to match the original)
Now, set the each factor equal to 0:
Do the same for the second factor:
Therefore, our two values of 


Alternatively, this problem can be solved by plugging each answer choice into the original equation and finding which set of numbers make the equation equate to 0.