Abstract Algebra
Help Questions
Abstract Algebra › Abstract Algebra
Which of the following is an ideal of a ring?
Maximal Ideal
Communicative Ideal
Minimal Ideal
Associative Ideal
None are ideals
Explanation
When dealing with rings there are three main ideals
Proper Ideal: When 




Prime Ideal: When 


Maximal Ideal: When 




Looking at the possible answer selections, Maximal Ideal is the correct answer choice.
Which of the following is an ideal of a ring?
Maximal Ideal
Communicative Ideal
Minimal Ideal
Associative Ideal
None are ideals
Explanation
When dealing with rings there are three main ideals
Proper Ideal: When 




Prime Ideal: When 


Maximal Ideal: When 




Looking at the possible answer selections, Maximal Ideal is the correct answer choice.
Identify the following definition.
Given that 






Line in
Circle in
Plane
Angle
Subfield
Explanation
By definition, given that 







Which of the following is an identity element of the binary operation 
Explanation
Defining the binary operation 
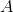


Then there exists an identity element 

Therefore, looking at the possible answer selections the correct answer is,
Which of the following is an identity element of the binary operation 
Explanation
Defining the binary operation 
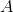


Then there exists an identity element 

Therefore, looking at the possible answer selections the correct answer is,
Which of the following is an identity element of the binary operation 
Explanation
Defining the binary operation 
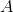


Then there exists an identity element 

Therefore, looking at the possible answer selections the correct answer is,
identify the following definition.
Given 




Factor Group
Simple Group
Subgroup
Normal Group
Cosets
Explanation
By definition of a factor group it is stated,
Given 






Which of the following is an ideal of a ring?
Maximal Ideal
Communicative Ideal
Minimal Ideal
Associative Ideal
None are ideals
Explanation
When dealing with rings there are three main ideals
Proper Ideal: When 




Prime Ideal: When 


Maximal Ideal: When 




Looking at the possible answer selections, Maximal Ideal is the correct answer choice.
Identify the following definition.
Given that 






Line in
Circle in
Plane
Angle
Subfield
Explanation
By definition, given that 







identify the following definition.
Given 




Factor Group
Simple Group
Subgroup
Normal Group
Cosets
Explanation
By definition of a factor group it is stated,
Given