How to interpret Venn diagrams
Help Questions
SSAT Upper Level Quantitative › How to interpret Venn diagrams

Examine the above Venn diagram. The universal set 


Explanation





The above Venn diagram represents all of this year's graduating seniors at Rockwell High School, the universal set 



Cathy was inducted into the National Honor Society in her junior year, and is still a member. She turned 18 on January 4 during her senior year, and she is carrying a respectable B average in her school's third-year French course. If her name were to be written in the above diagram in the correct place, in which of the five numbered regions would her name fall?
Explanation
Cathy is in the Honor Society, meaning that she is in set 




The above represents a Venn diagram. The universal set 
Let 


Explanation
The region in which 2,431 appears depends on the sets of which 2,431 is an element, which in turn depends on which of 7, 11, and 13 divides it evenly:
2,431 is a multiple of 11 and 13, but not 7, so 2,431 is in 









However:
2,145 is divisible by 11 and 13 but not 7, so this is the correct choice.

The universal set 
The subsets are:



How many elements are in the set represented by the shaded region?
Explanation
The shaded region is inside 


Examine 

so seventeen elements are in 
We eliminate all elements in 
This leaves twelve elements in 

Examine the above Venn diagram. The universal set 


Explanation














The universal set 


The subsets are:



How many elements are in the set represented by the shaded region?
The correct answer is not given among the other responses.
Explanation
The shaded region is 






To find ![c\left [ \left (A \cap C \right ) \cup \left (B \cap C \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/258895/gif.latex)
![c\left [ \left (A \cap C \right ) \cap \left (B \cap C \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/258896/gif.latex)



In the above Venn diagram, the universal set 



Which of the following Presidents would fall in the pink region?
Warren G. Harding, who was born on November 2, 1865 in Ohio and died during his third year in office.
Richard M. Nixon, who was born on January 9, 1913 in California and resigned during his seventh year in office,
Ronald Reagan, who was born on February 6, 1911 in Illinois and served eight years in office.
Woodrow Wilson, who was born on December 28, 1856 in New Jersey and served eight years in office.
Abraham Lincoln, who was born on February 12, 1809 in Kentucky and was shot to death during his fifth year in office.
Explanation
The shaded region is inside set 
The region is outside of 
The region is outside of 
The correct response is Harding.

A group of high school juniors are taking Biology, Calculus, and Spanish as shown above. Which student is not in the set 
Patrick
Molly
Bob
Steph
Andy
Explanation
The notation 


Giving the Venn diagram above, what is the sum of the numbers in the set 
Explanation
The notation 


When we add the numbers together, we get:
Given the Venn diagram below, which of the following does not belong to 
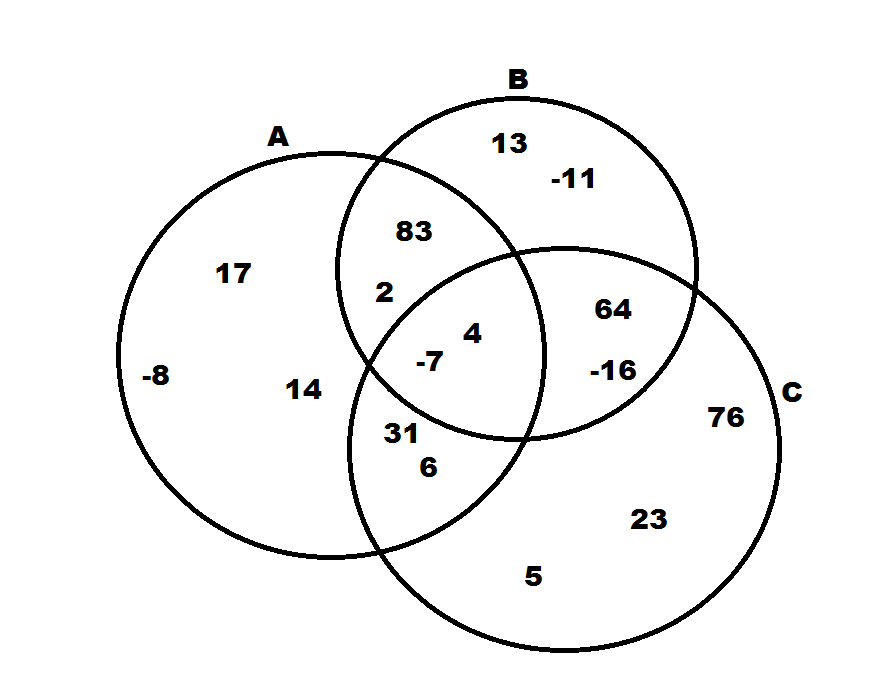
Explanation
The symbol 














































![c\left [ \left (A \cap C \right ) \cup \left (B \cap C \right ) \right ] = 2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/265841/gif.latex)
![c\left [ \left (A \cap C \right ) \cup \left (B \cap C \right ) \right ] = c \left (A \cap C \right )+ c \left (B \cap C \right )-c\left [ \left (A \cap C \right ) \cap \left (B \cap C \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/258899/gif.latex)












