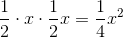How to find the area of a triangle
Help Questions
SSAT Middle Level Quantitative › How to find the area of a triangle
What is the area of the triangle?

Explanation
Area of a triangle can be determined using the equation:

Note: Figure NOT drawn to scale.
Refer to the above diagram. Give the ratio of the area of the green region to that of the white region.
The correct answer is not given among the other choices.
Explanation
The area of the entire rectangle is the product of its length and width, or

The area of the right triangle is half the product of its legs, or
The area of the green region is therefore the difference of the two, or

The ratio of the area of the green region to that of the white region is
That is, 11 to 4.

Note: Figure NOT drawn to scale.
What percent of the above figure is green?
The correct answer is not given among the other choices.
Explanation
The area of the entire rectangle is the product of its length and width, or

The area of the right triangle is half the product of its legs, or
The area of the green region is therefore the difference of the two, or

The green region is therefore
of the rectangle.
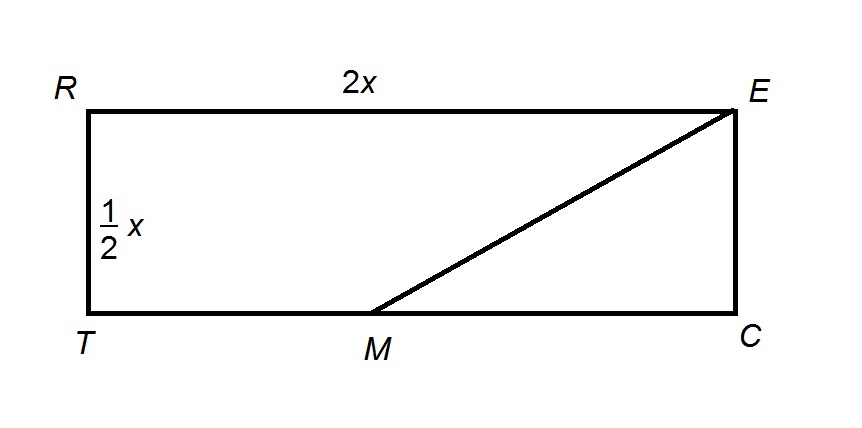
The above diagram shows Rectangle 


The area of 
Explanation





Its area is half their product, or
Set this equal to 225:


Give the perimeter of the above triangle in feet.
Explanation
The perimeter of the triangle - the sum of the lengths of its sides - is

Divide by 12 to convert to feet:
As a fraction, this is 

A triangle has a height of 9 inches and a base that is one third as long as the height. What is the area of the triangle, in square inches?
None of these
Explanation
The area of a triangle is found by multiplying the base times the height, divided by 2.
Given that the height is 9 inches, and the base is one third of the height, the base will be 3 inches.
We now have both the base (3) and height (9) of the triangle. We can use the equation to solve for the area.
The fraction cannot be simplified.

The quadrilateral in the above diagram is a square. What percent of it is white?
Explanation
The area of the entire square is the square of the length of a side, or

The area of the white right triangle is half the product of its legs, or

Therefore, the area of that triangle is
of that of the entire square.
The hypotenuse of a right triangle is 

Explanation
The area of a right triangle is half the product of the lengths of its legs, so we need to use the Pythagorean Theorem to find the length of the other leg. Set 
The legs have length 




Now find half the product:

Mr. Jones owns the isosceles-triangle-shaped parcel of land seen in the above diagram. He sells the parcel represented in red to his brother. What is the area of the land he retains?
Explanation
The area of a triangle is half the product of its base and its height, so Mr. Jones's parcel originally had area

The portion he sold his brother, represented by the red right triangle, has area

Therefore, the area of the parcel Mr. Jones retained is