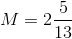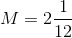How to find the length of the side of a right triangle
Help Questions
PSAT Math › How to find the length of the side of a right triangle

Note: Figure NOT drawn to scale.
Refer to the above diagram. Evaluate 
Explanation
The altitude perpendicular to the hypotenuse of a right triangle divides that triangle into two smaller triangles similar to each other and the large triangle. Therefore, the sides are in proportion. The hypotenuse of the triangle is equal to
Therefore, we can set up, and solve for 
The area of a right traingle is 42. One of the legs has a length of 12. What is the length of the other leg?
Explanation
A right triangle has sides of 36 and 39(hypotenuse). Find the length of the third side
33
42
15
12 √6
33√2
Explanation
use the pythagorean theorem:
a2 + b2 = c2 ; a and b are sides, c is the hypotenuse
a2 + 1296 = 1521
a2 = 225
a = 15
A right triangle with a base of 12 and hypotenuse of 15 is shown below. Find x.

3.5
4
4.5
5
5.5
Explanation
Using the Pythagorean Theorem, the height of the right triangle is found to be = √(〖15〗2 –〖12〗2) = 9, so x=9 – 5=4
A right triangle has two sides, 9 and x, and a hypotenuse of 15. What is x?
10
11
12
13
14
Explanation
We can use the Pythagorean Theorem to solve for x.
92 + _x_2 = 152
81 + _x_2 = 225
_x_2 = 144
x = 12
A right triangle has one side equal to 5 and its hypotenuse equal to 14. Its third side is equal to:
9
12
13.07
14.87
171
Explanation
The Pythagorean Theorem gives us _a_2 + _b_2 = _c_2 for a right triangle, where c is the hypotenuse and a and b are the smaller sides. Here a is equal to 5 and c is equal to 14, so _b_2 = 142 – 52 = 171. Therefore b is equal to the square root of 171 or approximately 13.07.
Which of the following could NOT be the lengths of the sides of a right triangle?
12, 16, 20
8, 15, 17
5, 7, 10
5, 12, 13
14, 48, 50
Explanation
We use the Pythagorean Theorem and we calculate that 25 + 49 is not equal to 100.
All of the other answer choices observe the theorem _a_2 + _b_2 = _c_2

If 


Explanation
AB is the leg adjacent to Angle A and BC is the leg opposite Angle A.
Since we have a 

Here, we know the side opposite the sixty degree angle. Thus, we can set that value equal to 
which also means
Solve for x.
6
7
12
2
Explanation
Use the Pythagorean Theorem. Let a = 8 and c = 10 (because it is the hypotenuse)
Which set of sides could make a right triangle?
6, 7, 8
4, 6, 9
9, 12, 15
10, 12, 16
Explanation
By virtue of the Pythagorean Theorem, in a right triangle the sum of the squares of the smaller two sides equals the square of the largest side. Only 9, 12, and 15 fit this rule.