Geometry
Help Questions
8th Grade Math › Geometry
Are the two shapes shown in the coordinate plane congruent? If so, what transformation did the red shape undergo from the orange shape?

No
Yes, translation to the left
Yes, 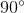
Yes, refection over the y-axis
Explanation
In order to solve this problem, we first need to know what "congruent" means. For two shapes to be congruent, they need to be the same shape and the same size. The shape can go through a transformation—rotation, translation, or reflection—but nothing else about the original shape can be changed for two shapes to be congruent.
Also, let's recall the types of transformations:
Rotation: A rotation means turning an image, shape, line, etc. around a central point.
Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.
Reflection: A reflection mean flipping an image, shape, line, etc. over a central line.
For this question, we can tell that the triangles are not the same size, the red triangle is smaller; thus, the triangles are not congruent.
Are the two shapes shown in the coordinate plane congruent? If so, what transformation did the red shape undergo from the orange shape?

Yes, translation to the left
Yes, reflection over the x-axis
Yes, 
No
Explanation
In order to solve this problem, we first need to know what "congruent" means. For two shapes to be congruent, they need to be the same shape and the same size. The shape can go through a transformation—rotation, translation, or reflection—but nothing else about the original shape can be changed for two shapes to be congruent.
Also, let's recall the types of transformations:
Rotation: A rotation means turning an image, shape, line, etc. around a central point.
Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.
Reflection: A reflection mean flipping an image, shape, line, etc. over a central line.
For this question, we can tell that the triangles are the same size; thus, the triangles are congruent. The red triangle has been moved to the left; thus, the triangle has been translated to the left.
The triangle has not undergone a reflection over the x-axis, because the triangle didn't flip over the x-axis. Also, the triangle has not been rotated 
In order to get to work, Jeff leaves home and drives 4 miles due north, then 3 miles due east, followed by 6 miles due north and, finally, 7 miles due east. What is the straight line distance from Jeff’s work to his home?
2√5
11
10√2
15
6√2
Explanation
Jeff drives a total of 10 miles north and 10 miles east. Using the Pythagorean theorem (a2+b2=c2), the direct route from Jeff’s home to his work can be calculated. 102+102=c2. 200=c2. √200=c. √100√2=c. 10√2=c
Calculate the volume of the cone provided. Round the answer to the nearest hundredth.

Explanation
In order to solve this problem, we need to recall the formula used to calculate the volume of a cone:
Now that we have this formula, we can substitute in the given values and solve:
Calculate the length of the missing side of the provided triangle. Round the answer to the nearest whole number.

Explanation
The provided triangle is a right triangle. We know this because the angle marker in the left corner of the triangle indicates that the triangle possesses a right or 
We can use the Pythagorean Theorem to help us solve this problem.
The Pythagorean Theorem states that for right triangles, the square of the hypotenuse is equal to the sum of the square of the other two sides. In other terms:

We can use the formula and substitute the known side lengths from the problem to solve for the missing side length:
Are the two shapes shown in the coordinate plane congruent? If so, what transformation did the red shape undergo from the orange shape?

No
Yes, translation down
Yes, 
Yes, refection over the x-axis
Explanation
In order to solve this problem, we first need to know what "congruent" means. For two shapes to be congruent, they need to be the same shape and the same size. The shape can go through a transformation—rotation, translation, or reflection—but nothing else about the original shape can be changed for two shapes to be congruent.
Also, let's recall the types of transformations:
Rotation: A rotation means turning an image, shape, line, etc. around a central point.
Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.
Reflection: A reflection mean flipping an image, shape, line, etc. over a central line.
For this question, we can tell that the triangles are not the same size, the red triangle is narrower; thus, the triangles are not congruent.
Are the two shapes shown in the coordinate plane congruent? If so, what transformation did the red shape undergo from the orange shape?

No
Yes, translation down and to the left
Yes, 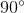
Yes, refection over the x-axis
Explanation
In order to solve this problem, we first need to know what "congruent" means. For two shapes to be congruent, they need to be the same shape and the same size. The shape can go through a transformation—rotation, translation, or reflection—but nothing else about the original shape can be changed for two shapes to be congruent.
Also, let's recall the types of transformations:
Rotation: A rotation means turning an image, shape, line, etc. around a central point.
Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.
Reflection: A reflection mean flipping an image, shape, line, etc. over a central line.
For this question, we can tell that the triangles are not the same size, the red triangle is smaller; thus, the triangles are not congruent.
In a right triangle, two sides have length 

Explanation
By the Pythagorean Theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Let 

Observe the location of the black and orange angles on the provided coordinate plane and identify which of the following transformations—rotation, translation, or reflection—the black angle has undergone in order to reach the position of the orange angle. Select the answer that provides the correct transformation shown in the provided image.

Translation down
A 
A reflection over the x-axis
Explanation
First, let's define the possible transformations.
Rotation: A rotation means turning an image, shape, line, etc. around a central point.
Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.
Reflection: A reflection mean flipping an image, shape, line, etc. over a central line.
In the images from the question, the line was not rotated 

If 


Not enough information to solve
Explanation
This problem is solved using the Pythagorean theorem 



Using the labels of our triangle we have:

































