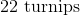SSAT Middle Level Quantitative - Ratio and Proportion

A soccer team played 20 games, winning 5 of them. The ratio of wins to losses is

$1\ to\ 3$

$1\ to\ 4$

$3\ to\ 1$

$4\ to\ 1$

$1\ to\ 5$

Explanation

The ratio of wins to losses requires knowing the number of wins and losses. The question says that there are 5 wins. That means there must have been

losses.

The ratio of wins to losses is thus 5 to 15 or 1 to 3.

A soccer team played 20 games, winning 5 of them. The ratio of wins to losses is

$1\ to\ 3$

$1\ to\ 4$

$3\ to\ 1$

$4\ to\ 1$

$1\ to\ 5$

Explanation

The ratio of wins to losses requires knowing the number of wins and losses. The question says that there are 5 wins. That means there must have been

losses.

The ratio of wins to losses is thus 5 to 15 or 1 to 3.

At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade turnips for ears of corn. If a man has ears of corn, then how many turnips can he get?

$351\ \text{turnips}$

$153\ \text{turnips}$

$531\ \text{turnips}$

$353\ \text{turnips}$

$533\ \text{turnips}$

Explanation

Ratios can be written in the following format:

$A:B\rightarrow \frac{A}{B}$

Using this format, substitute the given information to create a ratio.

$3\ \text{corn}: 13\ \text{turnips}$

Rewrite the ratio as a fraction.

$3\ \text{corn}: 13\ \text{turnips}\rightarrow \frac{3\ \text{corn}}{13\ \text{turnips}}$

We know that the farmer has ears of corn. Create a ratio with the variable that represents how many turnips he can get.

$\frac{81\ \text{corn}}{T}$

Create a proportion using the two ratios.

$\frac{3\ \text{corn}}{13\ \text{turnips}}=\frac{81\ \text{corn}}{T}$

Cross multiply and solve for .

$81\ \text{corn}\times 13\ \text{turnips}=3\ \text{corn}\times T$

Simplify.

Divide both sides of the equation by .

$\frac{3T}{3}=\frac{1053}{3}$

Solve.

The farmer can get $351\ \text{turnips}$ .

At a local microchip factory, there are managers for every workers. How many managers are needed for workers?

$20\ \text{managers}$

$21\ \text{managers}$

$19\ \text{managers}$

$18\ \text{managers}$

$16\ \text{managers}$

Explanation

In order to solve this problem, we will create a table of proportions using the following ratio.

$2\ \text{workers}: 5\ \text{managers}$

If we solve for the table, then we can find the number of managers needed for $50\ \text{workers}$ .

Table

The factory will need $20\ \text{managers}$ .

A motorcycle travels $723\textup{ miles}$ in $3\textup{ hours}$ . What is the motorcyclist’s speed in miles per hour (mph)?

$241\textup{ mph}$

$421\textup{ mph}$

$124\textup{ mph}$

$142\textup{ mph}$

$211\textup{ mph}$

Explanation

In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.

$723\ miles: 3\ hours=\frac{723\ miles}{3\ hours}$

Reduce and solve.

Write as a unit rate: revolutions in minutes

revolutions per minute

Explanation

Divide the number of revolutions by the number of minutes to get revolutions per minute:

$330\div 15 = 22$ ,

making revolutions per minute the correct choice.

At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade turnips for ears of corn. If a man has ears of corn, then how many turnips can he get?

$650\ \text{turnips}$

$750\ \text{turnips}$

$560\ \text{turnips}$

$550\ \text{turnips}$

$860\ \text{turnips}$

Explanation

Ratios can be written in the following format:

$A:B\rightarrow \frac{A}{B}$

Using this format, substitute the given information to create a ratio.

$3\ \text{corn}: 13\ \text{turnips}$

Rewrite the ratio as a fraction.

$3\ \text{corn}: 13\ \text{turnips}\rightarrow \frac{3\ \text{corn}}{13\ \text{turnips}}$

We know that the farmer has ears of corn. Create a ratio with the variable that represents how many turnips he can get.

$\frac{150\ \text{corn}}{T}$

Create a proportion using the two ratios.

$\frac{3\ \text{corn}}{13\ \text{turnips}}=\frac{150\ \text{corn}}{T}$

Cross multiply and solve for .

$150\ \text{corn}\times 13\ \text{turnips}=3\ \text{corn}\times T$

Simplify.

Divide both sides of the equation by .

$\frac{3T}{3}=\frac{1950}{3}$

Solve.

The farmer can get $650\ \text{turnips}$ .

At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade turnips for ears of corn. If a man has ears of corn, then how many turnips can he get?

$13000\ \text{turnips}$

$13113\ \text{turnips}$

$31000\ \text{turnips}$

$13013\ \text{turnips}$

$33000\ \text{turnips}$

Explanation

Ratios can be written in the following format:

$A:B\rightarrow \frac{A}{B}$

Using this format, substitute the given information to create a ratio.

$3\ \text{corn}: 13\ \text{turnips}$

Rewrite the ratio as a fraction.

$3\ \text{corn}: 13\ \text{turnips}\rightarrow \frac{3\ \text{corn}}{13\ \text{turnips}}$

We know that the farmer has ears of corn. Create a ratio with the variable that represents how many turnips he can get.

$\frac{3000\ \text{corn}}{T}$

Create a proportion using the two ratios.

$\frac{3\ \text{corn}}{13\ \text{turnips}}=\frac{3000\ \text{corn}}{T}$

Cross multiply and solve for .

$3000\ \text{corn}\times 13\ \text{turnips}=3\ \text{corn}\times T$

Simplify.

Divide both sides of the equation by .

$\frac{3T}{3}=\frac{39000}{3}$

Solve.

The farmer can get $13000\ \text{turnips}$ .

At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade turnips for ears of corn. If a man has ears of corn, then how many turnips can he get?