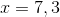Polynomials
Help Questions
SAT Math › Polynomials
Divide 

Explanation
It is not necessary to work a long division if you recognize 
A sum of cubes can be factored according to the pattern

so, setting 
Therefore,
Divide 

Explanation
It is not necessary to work a long division if you recognize 
A sum of cubes can be factored according to the pattern

so, setting 
Therefore,
Divide 

Explanation
It is not necessary to work a long division if you recognize 
A sum of cubes can be factored according to the pattern

so, setting 
Therefore,
Find the degree of the polynomial:
Explanation
To find the degree of a polynomial we must find the largest exponent in the function.
The degree of the polynomial 

Find the degree of the polynomial:
Explanation
To find the degree of a polynomial we must find the largest exponent in the function.
The degree of the polynomial 

Solve each problem and decide which is the best of the choices given.
What are the zeros of the following trinomial?
Explanation
First factor out a 


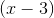
Set everything equal to zero and you get 



If a positive integer a is divided by 7, the remainder is 4. What is the remainder if 3_a_ + 5 is divided by 3?
2
3
4
5
6
Explanation
The best way to solve this problem is to plug in an appropriate value for a. For example, plug-in 11 for a because 11 divided by 7 will give us a remainder of 4.
Then 3_a + 5_, where a = 11, gives us 38. Then 38 divided by 3 gives a remainder of 2.
The algebra method is as follows:
a divided by 7 gives us some positive integer b, with a remainder of 4.
Thus,
a / 7 = b 4/7
a / 7 = (7_b +_ 4) / 7
a = (7_b_ + 4)
then 3_a + 5 =_ 3 (7_b_ + 4) + 5
(3_a_+5)/3 = \[3(7_b_ + 4) + 5\] / 3
= (7_b_ + 4) + 5/3
The first half of this expression (7_b_ + 4) is a positive integer, but the second half of this expression (5/3) gives us a remainder of 2.
If a positive integer a is divided by 7, the remainder is 4. What is the remainder if 3_a_ + 5 is divided by 3?
2
3
4
5
6
Explanation
The best way to solve this problem is to plug in an appropriate value for a. For example, plug-in 11 for a because 11 divided by 7 will give us a remainder of 4.
Then 3_a + 5_, where a = 11, gives us 38. Then 38 divided by 3 gives a remainder of 2.
The algebra method is as follows:
a divided by 7 gives us some positive integer b, with a remainder of 4.
Thus,
a / 7 = b 4/7
a / 7 = (7_b +_ 4) / 7
a = (7_b_ + 4)
then 3_a + 5 =_ 3 (7_b_ + 4) + 5
(3_a_+5)/3 = \[3(7_b_ + 4) + 5\] / 3
= (7_b_ + 4) + 5/3
The first half of this expression (7_b_ + 4) is a positive integer, but the second half of this expression (5/3) gives us a remainder of 2.
Find the degree of the polynomial:
Explanation
To find the degree of a polynomial we must find the largest exponent in the function.
The degree of the polynomial 

Solve each problem and decide which is the best of the choices given.
What are the zeros of the following trinomial?
Explanation
First factor out a 


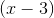
Set everything equal to zero and you get 









![x^{3} + (5y )^{3} =(x+5y) [x ^{2}+ x \cdot 5y + (5y)^{2}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/842425/gif.latex)