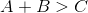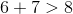Equilateral Triangles
Help Questions
SAT Math › Equilateral Triangles
What is the area of an equilateral triangle with sides 12 cm?
36√3
12√2
72√3
54√2
18√3
Explanation
An equilateral triangle has three congruent sides and results in three congruent angles. This figure results in two special right triangles back to back: 30° – 60° – 90° giving sides of x - x √3 – 2x in general. The height of the triangle is the x √3 side. So Atriangle = 1/2 bh = 1/2 * 12 * 6√3 = 36√3 cm2.
What is the area of an equilateral triangle with sides 12 cm?
36√3
12√2
72√3
54√2
18√3
Explanation
An equilateral triangle has three congruent sides and results in three congruent angles. This figure results in two special right triangles back to back: 30° – 60° – 90° giving sides of x - x √3 – 2x in general. The height of the triangle is the x √3 side. So Atriangle = 1/2 bh = 1/2 * 12 * 6√3 = 36√3 cm2.
The height of an equilateral triangle is
What is the triangle's perimeter?
12
24
6
8
Explanation
An altitude drawn in an equilateral triangle will form two 30-60-90 triangles. The height of equilateral triangle is the length of the longer leg of the 30-60-90 triangle. The length of the equilateral triangle's side is the length of the hypotenuse of the 30-60-90.
The ratio of the length of the hypotenuse to the length of the longer leg of a 30-60-90 triangle is
The length of the longer leg of the 30-60-90 triangle in this problem is
Using this ratio, we find that the length of this triangle's hypotenuse is 4. Thus the perimeter of the equilateral triangle will be 4 multiplied by 3, which is 12.
The height of an equilateral triangle is
What is the triangle's perimeter?
12
24
6
8
Explanation
An altitude drawn in an equilateral triangle will form two 30-60-90 triangles. The height of equilateral triangle is the length of the longer leg of the 30-60-90 triangle. The length of the equilateral triangle's side is the length of the hypotenuse of the 30-60-90.
The ratio of the length of the hypotenuse to the length of the longer leg of a 30-60-90 triangle is
The length of the longer leg of the 30-60-90 triangle in this problem is
Using this ratio, we find that the length of this triangle's hypotenuse is 4. Thus the perimeter of the equilateral triangle will be 4 multiplied by 3, which is 12.
In 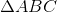



Explanation
The sum of the lengths of any two sides of a triangle must be greater than the length of third side.
Therefore, because
and


In 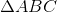



Explanation
The sum of the lengths of any two sides of a triangle must be greater than the length of third side.
Therefore, because
and


The area of square ABCD is 50% greater than the perimeter of the equilateral triangle EFG. If the area of square ABCD is equal to 45, then what is the area of EFG?
30
25√3
50
25
50√3
Explanation
If the area of ABCD is equal to 45, then the perimeter of EFG is equal to x * 1.5 = 45. 45 / 1.5 = 30, so the perimeter of EFG is equal to 30. This means that each side is equal to 10.
The height of the equilateral triangle EFG creates two 30-60-90 triangles, each with a hypotenuse of 10 and a short side equal to 5. We know that the long side of 30-60-90 triangle (here the height of EFG) is equal to √3 times the short side, or 5√3.
We then apply the formula for the area of a triangle, which is 1/2 * b * h. We get 1/2 * 10 * 5√3 = 5 * 5√3 = 25√ 3.
In general, the height of an equilateral triangle is equal to √3 / 2 times a side of the equilateral triangle. The area of an equilateral triangle is equal to 1/2 * √3s/ 2 * s = √3s2/4.
The area of square ABCD is 50% greater than the perimeter of the equilateral triangle EFG. If the area of square ABCD is equal to 45, then what is the area of EFG?
30
25√3
50
25
50√3
Explanation
If the area of ABCD is equal to 45, then the perimeter of EFG is equal to x * 1.5 = 45. 45 / 1.5 = 30, so the perimeter of EFG is equal to 30. This means that each side is equal to 10.
The height of the equilateral triangle EFG creates two 30-60-90 triangles, each with a hypotenuse of 10 and a short side equal to 5. We know that the long side of 30-60-90 triangle (here the height of EFG) is equal to √3 times the short side, or 5√3.
We then apply the formula for the area of a triangle, which is 1/2 * b * h. We get 1/2 * 10 * 5√3 = 5 * 5√3 = 25√ 3.
In general, the height of an equilateral triangle is equal to √3 / 2 times a side of the equilateral triangle. The area of an equilateral triangle is equal to 1/2 * √3s/ 2 * s = √3s2/4.
An equilateral triangle has a side length of 4. What is the height of the triangle?
Explanation
Because the triangle is an equilateral triangle, you know that all sides have the same length, so all sides have the length of 4. Draw the triangle and label all sides as 4. Next, draw a point in the middle of one of the sides, and label each side as 2. Draw a line segment from the midpoint that you just created to the opposite angle of the triangle. That line segment is the height of the triangle. You can solve for it by using the Pythagorean theorem.
The Pythagorean theorem states that
In our scenario a = 2, c = 4, and you are solving for b. After plugging the numbers into the formula you get
and then
and then
and then
Therefore, the height of the triangle is
An equilateral triangle has a side length of 4. What is the height of the triangle?
Explanation
Because the triangle is an equilateral triangle, you know that all sides have the same length, so all sides have the length of 4. Draw the triangle and label all sides as 4. Next, draw a point in the middle of one of the sides, and label each side as 2. Draw a line segment from the midpoint that you just created to the opposite angle of the triangle. That line segment is the height of the triangle. You can solve for it by using the Pythagorean theorem.
The Pythagorean theorem states that
In our scenario a = 2, c = 4, and you are solving for b. After plugging the numbers into the formula you get
and then
and then
and then
Therefore, the height of the triangle is