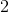Trapezoids
Help Questions
SAT Math › Trapezoids

The above figure shows Square 










Explanation
Construct 

Quadrilateral 

Since 

Since 



Substituting:
Apply the Product of Radicals and Quotient of Radicals Rules:

The above figure shows Square 










Explanation
Construct 

Quadrilateral 

Since 

Since 



Substituting:
Apply the Product of Radicals and Quotient of Radicals Rules:
A trapezoid has a base of length 4, another base of length s, and a height of length s. A square has sides of length s. What is the value of s such that the area of the trapezoid and the area of the square are equal?
Explanation
In general, the formula for the area of a trapezoid is (1/2)(a + b)(h), where a and b are the lengths of the bases, and h is the length of the height. Thus, we can write the area for the trapezoid given in the problem as follows:
area of trapezoid = (1/2)(4 + s)(s)
Similarly, the area of a square with sides of length a is given by _a_2. Thus, the area of the square given in the problem is _s_2.
We now can set the area of the trapezoid equal to the area of the square and solve for s.
(1/2)(4 + s)(s) = _s_2
Multiply both sides by 2 to eliminate the 1/2.
(4 + s)(s) = 2_s_2
Distribute the s on the left.
4_s_ + _s_2 = 2_s_2
Subtract _s_2 from both sides.
4_s_ = _s_2
Because s must be a positive number, we can divide both sides by s.
4 = s
This means the value of s must be 4.
The answer is 4.
A trapezoid has a base of length 4, another base of length s, and a height of length s. A square has sides of length s. What is the value of s such that the area of the trapezoid and the area of the square are equal?
Explanation
In general, the formula for the area of a trapezoid is (1/2)(a + b)(h), where a and b are the lengths of the bases, and h is the length of the height. Thus, we can write the area for the trapezoid given in the problem as follows:
area of trapezoid = (1/2)(4 + s)(s)
Similarly, the area of a square with sides of length a is given by _a_2. Thus, the area of the square given in the problem is _s_2.
We now can set the area of the trapezoid equal to the area of the square and solve for s.
(1/2)(4 + s)(s) = _s_2
Multiply both sides by 2 to eliminate the 1/2.
(4 + s)(s) = 2_s_2
Distribute the s on the left.
4_s_ + _s_2 = 2_s_2
Subtract _s_2 from both sides.
4_s_ = _s_2
Because s must be a positive number, we can divide both sides by s.
4 = s
This means the value of s must be 4.
The answer is 4.

The above figure shows Square 







If Square 


Explanation
Let 

Construct segment 


and

The area of Rectangle 
The lengths of the legs of Right 
and
The area of this right triangle is half the product of these lengths, or
This is seen below:

The sum of these areas is the area of Quadrilateral

Substituting 



The above figure shows Square 







If Square 


Explanation
Let 

Construct segment 


and

The area of Rectangle 
The lengths of the legs of Right 
and
The area of this right triangle is half the product of these lengths, or
This is seen below:

The sum of these areas is the area of Quadrilateral

Substituting 


Find the area of a trapezoid given bases of length 1 and 2 and height of 2.
Explanation
To solve, simply use the formula for the area of a trapezoid. Thus,
Find the area of a trapezoid given bases of length 1 and 2 and height of 2.
Explanation
To solve, simply use the formula for the area of a trapezoid. Thus,