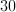Acute / Obtuse Isosceles Triangles
Help Questions
SAT Math › Acute / Obtuse Isosceles Triangles
The base angle of an isosceles triangle is 15 less than three times the vertex angle. What is the vertex angle?
Explanation
Every triangle contains 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes 
A triangle has the following side lengths:
Which of the following correctly describes the triangle?
Acute and isosceles
Obtuse and isosceles
Acute and scalene
Obtuse and scalene
None of these
Explanation
The triangle has two sides of equal length, 13, so it is by definition isosceles.
To determine whether the triangle is acute, right, or obtuse, compare the sum of the squares of the lengths of the two shortest sides to the square of the length of the longest side. The former quantity is equal to
The latter quantity is equal to
The former is greater than the latter; consequently, the triangle is acute. The correct response is that the triangle is acute and isosceles.
The base angle of an isosceles triangle is 15 less than three times the vertex angle. What is the vertex angle?
Explanation
Every triangle contains 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes 
A triangle has the following side lengths:
Which of the following correctly describes the triangle?
Acute and isosceles
Obtuse and isosceles
Acute and scalene
Obtuse and scalene
None of these
Explanation
The triangle has two sides of equal length, 13, so it is by definition isosceles.
To determine whether the triangle is acute, right, or obtuse, compare the sum of the squares of the lengths of the two shortest sides to the square of the length of the longest side. The former quantity is equal to
The latter quantity is equal to
The former is greater than the latter; consequently, the triangle is acute. The correct response is that the triangle is acute and isosceles.
The base angle of an isosceles triangle is five more than twice the vertex angle. What is the base angle?
Explanation
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes
Thus the vertex angle is 34 and the base angles are 73.
The base angle of an isosceles triangle is five more than twice the vertex angle. What is the base angle?
Explanation
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes
Thus the vertex angle is 34 and the base angles are 73.
An isosceles triangle has an area of 12. If the ratio of the base to the height is 3:2, what is the length of the two equal sides?
4
5
3√3
6
4√3
Explanation
Area of a triangle is ½ x base x height. Since base:height = 3:2, base = 1.5 height. Area = 12 = ½ x 1.5 height x height or 24/1.5 = height2. Height = 4. Base = 1.5 height = 6. Half the base and the height form the legs of a right triangle, with an equal leg of the isosceles triangle as the hypotenuse. This is a 3-4-5 right triangle.

An isosceles triangle has an area of 12. If the ratio of the base to the height is 3:2, what is the length of the two equal sides?
4
5
3√3
6
4√3
Explanation
Area of a triangle is ½ x base x height. Since base:height = 3:2, base = 1.5 height. Area = 12 = ½ x 1.5 height x height or 24/1.5 = height2. Height = 4. Base = 1.5 height = 6. Half the base and the height form the legs of a right triangle, with an equal leg of the isosceles triangle as the hypotenuse. This is a 3-4-5 right triangle.

Two sides of an isosceles triangle are 20 and 30. What is the difference of the largest and the smallest possible perimeters?
The answer cannot be determined
0
30
15
10
Explanation
The trick here is that we don't know which is the repeated side. Our possible triangles are therefore 20 + 20 + 30 = 70 or 30 + 30 + 20 = 80. The difference is therefore 80 – 70 or 10.
Two sides of an isosceles triangle are 20 and 30. What is the difference of the largest and the smallest possible perimeters?
The answer cannot be determined
0
30
15
10
Explanation
The trick here is that we don't know which is the repeated side. Our possible triangles are therefore 20 + 20 + 30 = 70 or 30 + 30 + 20 = 80. The difference is therefore 80 – 70 or 10.