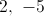How to use FOIL
Help Questions
SAT Math › How to use FOIL
Find the product in terms of 
Explanation
This question can be solved using the FOIL method. So the first terms are multiplied together:
This gives:
The x-squared is due to the x times x.
The outer terms are then multipled together and added to the value above.
The inner two terms are multipled together to give the next term of the expression.
Finally the last terms are multiplied together.
All of the above terms are added together to give:
Combining like terms gives

Solve for all real values of 
Explanation
First, move all terms to one side of the equation to set them equal to zero.
All terms contain an 
Now, we can factor the quadratic in parenthesis. We need two numbers that add to 

We now have three terms that multiply to equal zero. One of these terms must equal zero in order for the product to be zero.
Our answer will be 
x > 0.
Quantity A: (x+3)(x-5)(x)
Quantity B: (x-3)(x-1)(x+3)
Quantity A is greater
Quantity B is greater
The two quantities are equal
The relationship cannot be determined from the information given
Explanation
Use FOIL:
(x+3)(x-5)(x) = (x2 - 5x + 3x - 15)(x) = x3 - 5x2 + 3x2 - 15x = x3 - 2x2 - 15x for A.
(x-3)(x-1)(x+3) = (x-3)(x+3)(x-1) = (x2 + 3x - 3x - 9)(x-1) = (x2 - 9)(x-1)
(x2 - 9)(x-1) = x3 - x2 - 9x + 9 for B.
The difference between A and B:
(x3 - 2x2 - 15x) - (x3 - x2 - 9x + 9) = x3 - 2x2 - 15x - x3 + x2 + 9x - 9
= - x2 - 4x - 9. Since all of the terms are negative and x > 0:
A - B < 0.
Rearrange A - B < 0:
A < B
Expand the following expression:
Explanation
Expand the following expression:
Let's begin by recalling the meaning of FOIL: First, Outer, Inner, Last.
This means that in a situation such as we are given here, we need to multiply all the terms in a particular way. FOIL makes it easy to remember to multiply each pair of terms.
Let's begin:
First:
Outer:
Inner:
Last:
Now, put it together in standard form to get:
Factor 2x2 - 5x – 12
(x - 4) (2x + 3)
(x + 4) (2x + 3)
(x – 4) (2x – 3)
(x + 4) (2x + 3)
Explanation
Via the FOIL method, we can attest that x(2x) + x(3) + –4(2x) + –4(3) = 2x2 – 5x – 12.