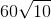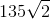How to find the perimeter of a hexagon
Help Questions
SAT Math › How to find the perimeter of a hexagon
A circle with circumference 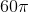
None of these
Explanation
Below is the figure referenced; note that the hexagon is divided by its diameters, and that an apothem—a perpendicular bisector from the center to one side—has been drawn.

The circle has circumference 


The hexagon is divided into six equilateral triangles. One, 








this makes the perimeter of the hexagon six times this, or


Archimedes High School has an unusual track in that it is shaped like a regular hexagon, as above. Each side of the hexagon measures 264 feet.
Alvin runs at a steady speed of seven miles an hour for twelve minutes, starting at point A and working his way clockwise. When he is finished, which of the following points is he closest to?
Point E
Point F
Point B
Point C
Point D
Explanation
Alvin runs at a rate of seven miles an hour for twelve minutes, or 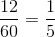


One mile comprises 5,280 feet, so this is equal to
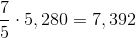
Since each side of the track measures 264 feet, this means that Alvin runs


which means that Alvin runs around the track four complete times, plus four more sides of the track. Alvin stops when he is at Point E.