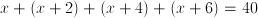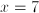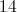How to find the number of integers between two other integers
Help Questions
SAT Math › How to find the number of integers between two other integers
The positive integer 
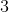
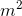





Explanation
We know that the remainder, 

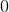


If 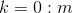

If 

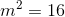



If 



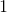
Thus, 
How many integers are between 

Explanation
An important consideration whenever you're asked for the number of integers between two other numbers is to determine whether the two "end points" are included. Here the word "inclusive" tells us that we need to count both -8 and 17 in our calculation.
A helpful tip for these questions: if you're including both end points, you can calculate by using the range (greatest value minus smallest value) and adding 1 to account for the inclusive set. (If you need to prove that to yourself, just use "how many integers between 1 and 3 inclusive" - clearly the set is 1, 2, 3 for three integers, but 3-1 = 2, so you can see you need to add one more to get the answer).
For this question, that leaves us with 17 - (8) = 25 as the range, and if you add 1 to that for "inclusive" you get the correct answer, 26.
Another way to look at this one is to chop it up: between -8 and 17 there are 8 negative integers (-1 through -8), 17 positive integers (1 through 17), and 0 as one more integer. 8 + 17 + 1 = 26.
Mrs. Lovell assigns her reading class to read pages three through sixty-four of their textbook. How many pages must each student read?
Explanation
To count the number of pages in between these two page numbers, we want to subtract 


Therefore, our answer is
How many integers lie between 

Explanation
Let's look at a small example, the numbers between 1 and 3 including all endpoints. We have 1, 2, and 3. If we subtract our numbers, we get 2. We need to add one more to get all the desired numbers. We can follow the same process with our larger numbers.
Take,

Then, adding 1,

Therefore, our answer is
Four consecutive odd integers sum to 40. How many of these numbers are prime?
Explanation
Let x equal the smallest of the four numbers. Therefore:
Therefore the four odd numbers are 7, 9, 11, and 13. Since all are prime except 9, three of the numbers are prime.
How many prime numbers are between 1 to 25?
Explanation
A prime numbers is a number greater than 1 that can only be divided by 1 and itself. Simply count from 1 to 25 and see how many values fit the criteria.
2, 3, 4, 5, 6, 7 , 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25
Prime numbers are underlined. Nine prime numbers are in this set interval.
A custom-made ruler is 

Explanation
There will be 15 gaps of