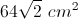How to find the area of a square
Help Questions
SAT Math › How to find the area of a square

Give the area of the provided square in square centimeters.
None of these
Explanation
The diagonal shown has length 6 meters; to convert to centimeters, multiply by 100:
The easiest way to find the area of the square given the length of a diagonal is to note that since a square is a rhombus, its area is equal to half the product of the lengths of its diagonals. Since one diagonal has length 600 centimeters, so does the other, and the area of the square is therefore
A square has the following perimeter:
Express its area in square meters.
None of these
Explanation
One meter comprises 100 centimeters, so divide the perimeter of the sides in centimeters by 100 to obtain the length in meters. This is the same as moving the decimal point left two spaces:
The perimeter of a square is equal to the sum of the lengths of its four equally long sides, so the length of one side is one fourth of - or, in decimal form, 0.25 times - its perimeter. For this square, this is:
The area of a square is equal to the square of the length of one side, so
One of the sides of a square on the coordinate plane has an endpoint at the point with coordinates 
None of the other responses gives a correct answer
Explanation
The length of a segment with endpoints 




This is the length of one side of the square, so the area is the square of this, or 117.
Find the area of a square with side length 4.
Explanation
To solve, simply use the formula for the area of a square.
Substitute the side length of four into the following equation.
Thus,
ABCD and EFGH are squares such that the perimeter of ABCD is 3 times that of EFGH. If the area of EFGH is 25, what is the area of ABCD?
5
15
25
75
225
Explanation
Assign variables such that
One side of ABCD = a
and One side of EFGH = e
Note that all sides are the same in a square. Since the perimeter is the sum of all sides, according to the question:
4a = 3 x 4e = 12e or a = 3e
From that area of EFGH is 25,
e x e = 25 so e = 5
Substitute a = 3e so a = 15
We aren’t done. Since we were asked for the area of ABCD, this is a x a = 225.
If the perimeter of a square is equal to twice its area, what is the length of one of its sides?
Explanation
Area of a square in terms of each of its sides:
Area = S x S
Perimeter of a square:
Perimeter = 4S
So if 'the perimeter of a square is equal to twice its area':
2 x Area = Perimeter
2 x \[S x S\] = \[4S\]; divide by 2:
S x S = 2S; divide by S:
S = 2
If the diagonal of a square measures 
Explanation
This is an isosceles right triangle, so the diagonal must equal 

A rhombus that is also a rectangle has a side length of 
Cannot be determined
Explanation
Remember that a rhombus that is also a rectangle is a square. Knowing that, the calculation is easy:
Find the area of a square whose side length is 5.
Explanation
To solve, simply use the formula for the area of a square. Thus,
Give the area of a square with the following perimeter:
Explanation
The perimeter of a square is equal to the sum of the lengths of its four equally long sides, so the length of one side is one fourth of its perimeter. For this square, this is:
12 inches are equal to one foot, so divide by 12 to convert to feet:
The area of a square is equal to the square of the length of one side, so