How to find the amount of rational numbers between two numbers
Help Questions
SAT Math › How to find the amount of rational numbers between two numbers
Two numbers have a greatest common divisor of 4 and a least common multiple of 40. How many different pairs of numbers are there that satisfy these properties?
Explanation
The greatest common divisor is 4. This means that both numbers must be divisible by 4. Furthermore, the least common multiple is 40, so both must divide 40.
The prime factorization of 40 is 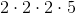
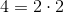
Now each number will have either two or three 2's and zero or one 5's. However, we also know that they can't both have three 2's, (since then the greatest common divisor would have three 2's as well). Similarly, only one can have a 5.
In essence, our problem becomes one of choice. We have 2 places with value 4. We choose to give a 5 to one of the two. We then give a 2 to one of the two. If we give a 5 and a 2 to the same side, we end up with 


Thus our two pairs are:
4,40 and 8,20