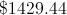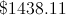How to find simple interest
Help Questions
SAT Math › How to find simple interest
Andrew received 


At the end of the year, Andrew earned a total of 










Explanation
Step 1: Set up the system of equations. Simple interest means that interest is calculated at the end of the year. Therefore, the amount of interest at the end of the year is the amount invested times the interest rate.
Let 
Let 
Step 2: Use substitution to solve the system.
Substitute 


Step 3: Solve for 
Peter wanted to buy a car and borrowed \$2,500 from the bank at 5% simple interest per year. He was able to pay back the loan in one lump sum at six months. What was the total amount he paid the bank?
Explanation
Simple interest is given by 




Remember, six months is the same as half of a year. The total paid back to the bank is the principle plus the interest, or \$2,562.50.
You really want to buy a car that costs \$15,000 but you only have \$5,000 saved. Rather than getting a bank loan, your parents offer to lend you the extra money but will require you to pay them back with 4.3% interest. How much will car cost in total after you have paid your parents back?
Explanation
Amount borrowed = $15,000 – $5,000 = \$10,000
Interest of 4.3% = \$10,000 * 0.043 = \$430
Total cost of car = \$5000 + $10000 + $430 = \$15,430
Ted works over the summer and makes \$9 per hour. He works for 20 hours each week for 10 weeks. After paying 10% in taxes, he buys a bike for \$500 and puts the rest of his money in the bank.
If Ted's bank pays 5% interest on the total sum once per year, and Ted doesn't add or remove anything from the account, how much money (rounded to the nearest cent) will Ted have in 5 years?
Explanation
To start, we see that Ted works for 20 hours per week for 10 weeks. This means he works a total of 200 hours over the summer. He is paid \$9 dollars each hour. Therefore he makes \$9 x 200 hours = \$1800 total over the summer. He then has to pay 10% in taxes, or .1 x \$1800, leaving him with 
Now we have to find out how much he will have 5 years later. Since the bank pays 5% interest each year, we know that he will make 5% of what he has each year. He starts with \$1,120. 5% of this value is 
This is also the same as multiplying instead by 1.05. We repeat this step 5 times, giving us:
I have \$100 in my bank. After one year, I have withdrawn a total of \$20 and I still have \$85 in the bank. What is the yearly interest rate of my bank account?
Explanation
Since I have withdrawn \$20, that means I only have \$80 in my account.

which is 6.25%.
Dan took out a \$1200 loan at a rate of 3% simple interest a year. What is the amount of interest accrued for one month?
Explanation
\$1200 is the amount that he took out.
3% annually would yield an interest amount of \$36.
Therefore, each month, he would be paying \$3 a month.
A student puts 


Explanation
Simple interest is calculated using the following formula:
Where



For this problem, that means:
If a student borrows \$200,000 at an interest rate of 6% compounded annually, when she graduates in 4 years how much money will she owe? Round to the nearest dollar.
Explanation
This problem requires knowledge of the compound interest formula,
Where 




We know that the student borrowed \$200,000 compounded annually at a 6% interest rate, therefore by plugging in those numbers we find that after she graduates in 4 years she will owe \$252,495.
You invest \$1000 in a bank that gives 5% interest every year on the money in your account. How much interest do you make in 3 years (to the nearest dollar)?
Explanation
Step 1: We need to convert 


Step 2: Calculate Simple interest and ending balance for 1 year.
Interest=
Ending Balance=
Step 3: Calculate Simple interest and ending balance for the next year (2nd year)
Interest=
Ending Balance=
Step 4: Calculate Simple Interest and ending balance of the third and final year
Interest=
Ending Balance=
Step 5: Add up the interest calculations:

If a student borrows \$200,000 at an interest rate of 6% compounded quarterly, when she graduates in 4 years how much money will she owe? Round to the nearest dollar.
Explanation
This problem requires knowledge of the compound interest formula,
Where 




We know that the student borrowed \$200,000 compounded quarterly at a 6% interest rate, therefore by plugging in those numbers we find what she will owe after she graduates in 4 years.