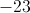How to find consecutive integers
Help Questions
SAT Math › How to find consecutive integers
The sum of four consecutive odd integers is equal to 96. How many of the integers are prime?
0
1
2
3
4
Explanation
Let x be the smallest of the four integers. We are told that the integers are consecutive odd integers. Because odd integers are separated by two, each consecutive odd integer is two larger than the one before it. Thus, we can let x + 2 represent the second integer, x + 4 represent the third, and x + 6 represent the fourth. The sum of the four integers equals 96, so we can write the following equation:
x + (x + 2) + (x + 4) + (x + 6) = 96
Combine x terms.
4_x_ + 2 + 4 + 6 = 96
Combine constants on the left side.
4_x_ + 12 = 96
Subtract 12 from both sides.
4_x_ = 84
Divide both sides by 4.
x = 21
This means the smallest integer is 21. The other integers are therefore 23, 25, and 27.
The question asks us how many of the four integers are prime. A prime number is divisible only by itself and one. Among the four integers, only 23 is prime. The number 21 is divisible by 3 and 7; the number 25 is divisible by 5; and 27 is divisible by 3 and 9. Thus, 23 is the only number from the integers that is prime. There is only one prime integer.
The answer is 1.
Explanation
In the repeating pattern 9,5,6,2,1,9,5,6,2,1......What is the 457th number in the sequence?
5
9
1
2
1
Explanation
There are 5 numbers in the sequnce.
How many numbers are left over if you divide 5 into 457?
There would be 2 numbers!
The second number in the sequence is 9,5,6,2,1
Four consecutive integers have a mean of 9.5. What is the largest of these integers?
12
13
9
8
11
Explanation
Four consecutive integers could be represented as n, n+1, n+2, n+3
Therefore, by saying that they have a mean of 9.5, we mean to say:
(n + n+1 + n+2 + n+ 3)/4 = 9.5
(4n + 6)/4 = 9.5 → 4n + 6 = 38 → 4n = 32 → n = 8
Therefore, the largest value is n + 3, or 11.
Four consecutive odd integers have a sum of 32. What are the integers?
Explanation
Consecutive odd integers can be represented as x, x+2, x+4, and x+6.
We know that the sum of these integers is 32. We can add the terms together and set it equal to 32:
x + (x+2) + (x+4) + (x+6) = 32
4x + 12 = 32
4x = 20
x = 5; x+2=7; x+4 = 9; x+6 = 11
Our integers are 5, 7, 9, and 11.
The sum of three consecutive even integers equals 72. What is the product of these integers?
13728
12144
10560
13800
17472
Explanation
Let us call x the smallest integer. Because the next two numbers are consecutive even integers, we can call represent them as x + 2 and x + 4. We are told the sum of x, x+2, and x+4 is equal to 72.
x + (x + 2) + (x + 4) = 72
3x + 6 = 72
3x = 66
x = 22.
This means that the integers are 22, 24, and 26. The question asks us for the product of these numbers, which is 22(24)(26) = 13728.
The answer is 13728.
The sum of three consecutive integers is 60. Find the smallest of these three integers.
Explanation
Assume the three consecutive integers equal 


The sum of three consecutive even integers is 108. What is the largest number?
34
36
38
40
42
Explanation
Three consecutive even integers can be represented by x, x+2, x+4. The sum is 3x+6, which is equal to 108. Thus, 3x+6=108. Solving for x yields x=34. However, the question asks for the largest number, which is x+4 or 38. Please make sure to answer what the question asks for!
You could have also plugged in the answer choices. If you plugged in 38 as the largest number, then the previous even integer would be 36 and the next previous even integer 34. The sum of 34, 36, and 38 yields 108.
If 


Explanation
Since 
What we notice, however, is that for