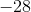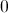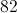How to find absolute value
Help Questions
SAT Math › How to find absolute value
Let 




Explanation
We need to solve the two equations |2a – 3| = 5 and |3 – 4b| = 11, in order to determine the possible values of a and b. When solving equations involving absolute values, we must remember to consider both the positive and negative cases. For example, if |x| = 4, then x can be either 4 or –4.
Let's look at |2a – 3| = 5. The two equations we need to solve are 2a – 3 = 5 and 2a – 3 = –5.
2a – 3 = 5 or 2a – 3 = –5
Add 3 to both sides.
2a = 8 or 2a = –2
Divide by 2.
a = 4 or a = –1
Therefore, the two possible values for a are 4 and –1. However, the problem states that both a and b are negative. Thus, a must equal –1.
Let's now find the values of b.
3 – 4b = 11 or 3 – 4b = –11
Subtract 3 from both sides.
–4b = 8 or –4b = –14
Divide by –4.
b = –2 or b = 7/2
Since b must also be negative, b must equal –2.
We have determined that a is –1 and b is –2. The original question asks us to find |b – a|.
|b – a| = |–2 – (–1)| = | –2 + 1 | = |–1| = 1.
The answer is 1.
Which of the following sentences is represented by the equation
The absolute value of the sum of a number and seven is three less than the number.
The absolute value of the sum of a number and seven is three greater than the number.
The sum of three and the absolute value of the sum of a number is three greater than the number.
The sum of three and the absolute value of the sum of a number is three less than the number.
None of the other responses are correct.
Explanation




"The absolute value of the sum of a number and seven is three less than the number."
Evaluate for 
Explanation
Substitute 0.6 for 
If 

Explanation
Substitute – 4 in for x. Remember that when a negative number is raised to the third power, it is negative. - = – 64. – 64 – 36 = – 100. Since you are asked to take the absolute value of – 100 the final value of f(-4) = 100. The absolute value of any number is positive.
Solve:
Explanation
To solve this problem, we want to set what's inside the absolute value signs equal to the positive and negative value on the right side of the equation. That's because the value inside the absolute value symbols could be equivalent to 

So let's set 


First:
Second:
Therefore, our answers are 

Define an operation 
For all real numbers 
Evaluate: 
The expression is undefined.
None of the other responses is correct.
Explanation

Find the absolute value of the following expression:
Explanation
In order the find the answer, you must first solve what is inside the absolute value signs.
Following order of operations, you must first multiply 

Then you must subtract 

Now, you must take the absolute value of 

Evaluate the expression if 

Explanation
To solve, we replace each variable with the given value.
Simplify. Remember that terms inside of the absolute value are always positive.
Evaluate for 
Explanation
Simplify the following:
Explanation
Simplify the following:
Begin with basic subtraction:
Next, remember what we do with absolute value signs; we change negative values to positive values, and positive values remain positive.
So our answer is positive 51