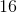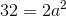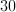Plane Geometry
Help Questions
SAT Math › Plane Geometry
Two chords of a circle, 






Give the length of 
Insufficient information is given to find the length of 
Explanation
Let 




If two chords intersect inside the circle, then they cut each other in such a way that the product of the lengths of the parts is the same for the two chords - that is,
Substituting the appropriate quantities, then solving for 
This statement is identically true. Therefore, without further information, we cannot determine the value of 

The length of the diagonal of a given square is 
Explanation
If we divide the square into two triangles via its diagonal, then we know that the length of the diagonal is equal to the length of the triangles' hypotenuse.
We can use the Pythagorean Theorem to find the length of the two sides of one of our triangles.
Since we're dealing with a square, we know that the two sides of the square (which are the same as the two sides of one of our triangles) will be equal to one another. Therefore, we can say:
Now, solve for the unknown:

This means that the length of the sides of our triangle, as well as the sides of our square, is 
To find the area of the square, do the following:

A triangle has the following side lengths:
Which of the following correctly describes the triangle?
Acute and isosceles
Obtuse and isosceles
Acute and scalene
Obtuse and scalene
None of these
Explanation
The triangle has two sides of equal length, 13, so it is by definition isosceles.
To determine whether the triangle is acute, right, or obtuse, compare the sum of the squares of the lengths of the two shortest sides to the square of the length of the longest side. The former quantity is equal to
The latter quantity is equal to
The former is greater than the latter; consequently, the triangle is acute. The correct response is that the triangle is acute and isosceles.
The base angle of an isosceles triangle is 15 less than three times the vertex angle. What is the vertex angle?
Explanation
Every triangle contains 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes 
What is the area of a square that has a diagonal whose endpoints in the coordinate plane are located at (-8, 6) and (2, -4)?
100
100√2
50√2
50
200√2
Explanation
The length of the diagonal of a given square is 
Explanation
If we divide the square into two triangles via its diagonal, then we know that the length of the diagonal is equal to the length of the triangles' hypotenuse.
We can use the Pythagorean Theorem to find the length of the two sides of one of our triangles.
Since we're dealing with a square, we know that the two sides of the square (which are the same as the two sides of one of our triangles) will be equal to one another. Therefore, we can say:
Now, solve for the unknown:

This means that the length of the sides of our triangle, as well as the sides of our square, is 
To find the area of the square, do the following:

A regular seven sided polygon has a side length of 14”. What is the measurement of one of the interior angles of the polygon?
128.57 degrees
257.14 degrees
180 degrees
154.28 degrees
252 degrees
Explanation
The formula for of interior angles based on a polygon with a number of side n is:
Each Interior Angle = (n-2)*180/n
= (7-2)*180/7 = 128.57 degrees
Solve each problem and decide which is the best of the choices given.
If 

Explanation
This is a 
Remembering that

Thus,

If 

Thus, making

A square with a side length of 4 inches is inscribed in a circle, as shown below. What is the area of the unshaded region inside of the circle, in square inches?

8π - 16
4π-4
8π-4
2π-4
8π-8
Explanation
Using the Pythagorean Theorem, the diameter of the circle (also the diagonal of the square) can be found to be 4√2. Thus, the radius of the circle is half of the diameter, or 2√2. The area of the circle is then π(2√2)2, which equals 8π. Next, the area of the square must be subtracted from the entire circle, yielding an area of 8π-16 square inches.
What is the hypotenuse of a right triangle with side lengths 

Explanation
The Pythagorean Theorem states that . This question gives us the values of



Take 



Now we can start solving for 
The length of the hypotenuse is