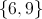Venn Diagrams
Help Questions
SAT Math › Venn Diagrams

In the above Venn diagram, let the universal set be


How many elements of 
Six
Seven
Eight
Nine
Five
Explanation
The shaded portion of the Venn diagram is 


The following elements of 

If 3 is subtracted from each, what results are the elements whose division by 4 yields a remainder of 1, and thus, elements of 
The following elements of 

The elements in 



In the above Venn diagram, let the universal set be


How many elements of 
Six
Seven
Eight
Nine
Five
Explanation
The shaded portion of the Venn diagram is 


The following elements of 

If 3 is subtracted from each, what results are the elements whose division by 4 yields a remainder of 1, and thus, elements of 
The following elements of 

The elements in 



In the above Venn diagram, let the universal set be


How many elements of 
Six
Seven
Eight
Nine
Five
Explanation
The shaded portion of the Venn diagram is 


The following elements of 

If 3 is subtracted from each, what results are the elements whose division by 4 yields a remainder of 1, and thus, elements of 
The following elements of 

The elements in 




Find 
Explanation
The intersection of two sets contains every element that is present in both sets, so 


Find 
Explanation
The intersection of two sets contains every element that is present in both sets, so 


Find 
Explanation
The intersection of two sets contains every element that is present in both sets, so 
We have two sports clubs offered to a class of 100 students. 70 students joined the basketball club, 40 students joined the swimming club, and 10 students joined neither. How many students joined both the swimming club and the basketball club?
Explanation
The idea is to draw a Venn Diagram and find the intersection. We have one circle of 70 and another with 40. When we add the two circles plus the 10 students who joined neither, we should get 100 students. However, when adding the two circles, we are adding the intersections twice, therefore we need to subtract the intersection once.
We get 
What is the intersection of the Venn Diagram shown below?

Explanation
The intersection of the Venn Diagram is only the numbers in both circles.
The section in the middle contains the answer set.
Thus the intersection is, 
We have two sports clubs offered to a class of 100 students. 70 students joined the basketball club, 40 students joined the swimming club, and 10 students joined neither. How many students joined both the swimming club and the basketball club?
Explanation
The idea is to draw a Venn Diagram and find the intersection. We have one circle of 70 and another with 40. When we add the two circles plus the 10 students who joined neither, we should get 100 students. However, when adding the two circles, we are adding the intersections twice, therefore we need to subtract the intersection once.
We get 
Set A contains the positive even integers less than 14. Set B contains the positive multiples of three less than 20. What is the intersection of the two sets?
A∩B = { }
A∩B = {6, 12}
A∩B = {4, 6, 8}
A∩B = {6}
A∩B = {6, 12, 18}
Explanation
A = {2, 4, 6, 8, 10, 12}
B = {3, 6, 9, 12, 15, 18}
The intersection of a set means that the elements are in both sets: A∩B = {6, 12}