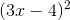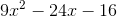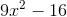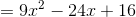Algebra

Help Questions

SAT Math › Algebra

Questions 1 - 10

According to Heron's Formula, the area of a triangle with side lengths of a, b, and c is given by the following:

Hero

where s is one-half of the triangle's perimeter.

What is the area of a triangle with side lengths of 6, 10, and 12 units?

12√5

4√14

8√14

14√2

48√77

Explanation

We can use Heron's formula to find the area of the triangle. We can let a = 6, b = 10, and c = 12.

In order to find s, we need to find one half of the perimeter. The perimeter is the sum of the lengths of the sides of the triangle.

Perimeter = a + b + c = 6 + 10 + 12 = 28

In order to find s, we must multiply the perimeter by one-half, which would give us (1/2)(28), or 14.

Now that we have a, b, c, and s, we can calculate the area using Heron's formula.

Hero

Hero2

Find the product of (3 + 4i)(4 - 3i) given that i is the square root of negative one.

7 + i

12 - 12i

24 + 7i

Explanation

Distribute (3 + 4i)(4 - 3i)

3(4) + 3(-3i) + 4i(4) + 4i(-3i)

12 - 9i + 16i -12i2

12 + 7i - 12(-1)

12 + 7i + 12

24 + 7i

Pets Plus makes bird houses. Their monthly fixed expenses are $750. The cost for each bird house is $15. The bird houses sell for $40.

If Pets Plus sells 50 bird houses, what is the profit?

$$500$

$$250$

$$750$

$$300$

$$625$

Explanation

Let $x$ = the number of birdhouses sold each month.

$Revenue=40x$

$Costs=15x+750$

$Profit = Revenue-Costs$

$=40x-15x-750$

$=25x-750$

Substituting in 50 for $x$ gives an answer of 500, so the profit on 50 birdhouses is $500.

Simplify:

Explanation

If you don't already have the pattern memorized, use FOIL. It's best to write out the parentheses twice (as below) to avoid mistakes:

Evaluate

$3^{21}$

$3^{27}$

$3^{10}$

$3^{14}$

Explanation

When adding exponents, we don't multiply the exponents but we try to factor to see if we simplify the addition problem. In this case, we can simplify it by factoring . We get .

If , then $\frac{(c^3)^2}{c^2c^4}=?$

Cannot be determined

Explanation

Start by simplifying the numerator and denominator separately. In the numerator, (c3)2 is equal to c6. In the denominator, c2 * c4 equals c6 as well. Dividing the numerator by the denominator, c6/c6, gives an answer of 1, because the numerator and the denominator are the equivalent.

Solve for .

$\frac{1}{3}(3x-6)+\frac{1}{2}(2x+4)=\frac{1}{5}(15x -5)$

$-2$

$-3$

$0$

$2$

Explanation

First distribute the fractions:

Combine like terms:

The sum of four consecutive even integers is , but their product is . What is the least of those integers?

Explanation

Any time the product of consecutive numbers is , must be a one of those consecutive numbers, because if it is not, the product will be non-zero. This leaves us with four possibilities, depending on where is placed in the sequence.

As we can see, , , and are our numbers in question, meaning is our answer as the lowest number.

Note that it is possible to use algebra and set up a system of equations, but it's more time-consuming, which could hinder more than help in a standardized test setting.

Factor the following equation.

x2 – 16

(x + 4)(x + 4)

(x – 4)(x – 4)

(x + 4)(x – 4)

(x)(x – 4)

(x2)(4 – 2)

Explanation

The correct answer is (x + 4)(x – 4)

We neen to factor x2 – 16 to solve. We know that each parenthesis will contain an x to make the x2. We know that the root of 16 is 4 and since it is negative and no value of x is present we can tell that one 4 must be positive and the other negative. If we work it from the multiple choice answers we will see that when multiplying it out we get x2 + 4x – 4x – 16. 4x – 4x cancels out and we are left with our answer.

Given $9 \cdot 3^n = 3^9$ , what is the value of ?