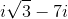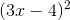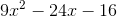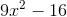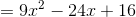Exponents
Help Questions
SAT Math › Exponents
Simplify:
Explanation
Use FOIL:
Combine like terms:
But since 
Simplify:
Explanation
Rewrite 
Simplify:
Explanation
If you don't already have the pattern memorized, use FOIL. It's best to write out the parentheses twice (as below) to avoid mistakes:
If
and

what is the value of a?
Explanation
When dividing exponents,

Therefore,

If 

We can now solve the system of equations 

If we solve for a in the first equation and plug it into the second equation, we get 

If we substitute this value of b into the first equation, we can solve for a and find that 
Solve:
Explanation
When dividing expressions with the same variable, combine terms by subtracting the exponents, while leaving the variable unchanged. For this problem, we do that by subtracting 3-5, to get a new exponent of -2. However, because the exponent is negative, we can place the new expression in the denominator of the fraction and make the exponent positive:
Solve:
Explanation
When dividing expressions with the same variable, combine terms by subtracting the exponents, while leaving the variable unchanged. For this problem, we do that by subtracting 6-2, to get a new exponent of 4:
Simplify:
Explanation
Although we have different bases, we know that 
Therefore,

Finally, we factor out 

If 
Cannot be determined
Explanation
Start by simplifying the numerator and denominator separately. In the numerator, (c3)2 is equal to c6. In the denominator, c2 * c4 equals c6 as well. Dividing the numerator by the denominator, c6/c6, gives an answer of 1, because the numerator and the denominator are the equivalent.
Explanation
When dividing exponents, we need to make sure we have the same base. In this case we do. Then we just subtract the exponents. The answer is 
Explanation
The key to this problem is understanding how exponents divide. When two exponents have the same base, then the exponent on the bottom can simply be subtracted from the exponent on top. I.e.:
Keeping this in mind, we simply break the problem down into prime factors, multiply out the exponents, and solve.