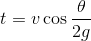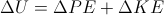Linear Motion
Help Questions
SAT Subject Test in Physics › Linear Motion
Near the surface of the earth, a projectile is fired from a canon at an angle of 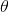

Explanation
At the maximum height of projectile motion, 

We can then rearrange for
Next substitute this value into the equation 
Near the surface of the earth, a projectile is fired from a canon at an angle of 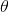

Explanation
At the maximum height of projectile motion, 

We can then rearrange for
Next substitute this value into the equation 
Near the surface of the earth, a projectile is fired from a canon at an angle of 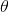

Explanation
At the maximum height of projectile motion, 

We can then rearrange for
Next substitute this value into the equation 
If air resistance is negligible, 8 seconds after it is released, what would be the velocity of a stone dropped from a helicopter that has a horizontal velocity of 60 meters per second?
Explanation
We are looking for total velocity, which in this case has both a horizontal and vertical component.
Because the helicopter is flying horizontally we know
We can assume that this takes place near the surface of the earth so
We can plug this into the equation:
Next we must find the horizontal velocity. Because there are no additional forces, the horizontal velocity is the same as the initial horizontal velocity of the helicopter, so:
Next we must use vector addition to add the horizontal and vertical components of velocity. Because this horizontal and vertical velocities are perpendicular the sum will be the hypotenuse of a right triangle:

If air resistance is negligible, 8 seconds after it is released, what would be the velocity of a stone dropped from a helicopter that has a horizontal velocity of 60 meters per second?
Explanation
We are looking for total velocity, which in this case has both a horizontal and vertical component.
Because the helicopter is flying horizontally we know
We can assume that this takes place near the surface of the earth so
We can plug this into the equation:
Next we must find the horizontal velocity. Because there are no additional forces, the horizontal velocity is the same as the initial horizontal velocity of the helicopter, so:
Next we must use vector addition to add the horizontal and vertical components of velocity. Because this horizontal and vertical velocities are perpendicular the sum will be the hypotenuse of a right triangle:

If air resistance is negligible, 8 seconds after it is released, what would be the velocity of a stone dropped from a helicopter that has a horizontal velocity of 60 meters per second?
Explanation
We are looking for total velocity, which in this case has both a horizontal and vertical component.
Because the helicopter is flying horizontally we know
We can assume that this takes place near the surface of the earth so
We can plug this into the equation:
Next we must find the horizontal velocity. Because there are no additional forces, the horizontal velocity is the same as the initial horizontal velocity of the helicopter, so:
Next we must use vector addition to add the horizontal and vertical components of velocity. Because this horizontal and vertical velocities are perpendicular the sum will be the hypotenuse of a right triangle:

Which of these is not an example of Newtonian mechanics?
Explanation
Newtonian mechanics apply to all objects of substantial mass travelling at significantly slower than the speed of light.
Newton's law of universal gravitation, Newton's second law, momentum, and the equation for mechanical energy all fall under Newtonian mechanics.
The mass-energy equivalence suggests that mass can change as the speed of an object (such as an electron) approaches the speed of light. Newtonian mechanics assume that mass is constant, and do not apply to objects approaching the speed of light.
Which of these is not an example of Newtonian mechanics?
Explanation
Newtonian mechanics apply to all objects of substantial mass travelling at significantly slower than the speed of light.
Newton's law of universal gravitation, Newton's second law, momentum, and the equation for mechanical energy all fall under Newtonian mechanics.
The mass-energy equivalence suggests that mass can change as the speed of an object (such as an electron) approaches the speed of light. Newtonian mechanics assume that mass is constant, and do not apply to objects approaching the speed of light.
Sam throws a 



At what angle to the horizontal will the rock impact the ground?
Explanation
The question gives the total initial velocity, but we will need to find the horizontal and vertical components.
To find the horizontal velocity we use the equation 
We can plug in the given values for the angle and initial velocity to solve.
We can find the vertical velocity using the equation 
The horizontal velocity will not change during flight because there are no forces in the horizontal direction. The vertical velocity, however, will be affected. We need to solve for the final vertical velocity, then combine the vertical and horizontal vectors to find the total final velocity.
We know that the rock is going to travel a net distance of 
Because the rock is traveling downward, our velocity will be negative: 
Now that we know our final velocities in both the horizontal and vertical directions, we can find the angle created between the two trajectories. The horizontal and vertical velocities can be compared using trigonometry.

Plug in our values and solve for the angle.
Sam throws a 



At what angle to the horizontal will the rock impact the ground?
Explanation
The question gives the total initial velocity, but we will need to find the horizontal and vertical components.
To find the horizontal velocity we use the equation 
We can plug in the given values for the angle and initial velocity to solve.
We can find the vertical velocity using the equation 
The horizontal velocity will not change during flight because there are no forces in the horizontal direction. The vertical velocity, however, will be affected. We need to solve for the final vertical velocity, then combine the vertical and horizontal vectors to find the total final velocity.
We know that the rock is going to travel a net distance of 
Because the rock is traveling downward, our velocity will be negative: 
Now that we know our final velocities in both the horizontal and vertical directions, we can find the angle created between the two trajectories. The horizontal and vertical velocities can be compared using trigonometry.

Plug in our values and solve for the angle.