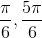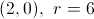SAT Subject Test in Math II
Help Questions
SAT Math › SAT Subject Test in Math II
Solve for 
![[0,2\pi]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/235309/gif.latex)
Explanation
First we must solve for when sin is equal to 1/2. That is at
Now, plug it in:
A circle with a radius of five is centered at the origin. A point on the circumference of the circle has an x-coordinate of two and a positive y-coordinate. What is the value of the y-coordinate?
Explanation
Recall that the general form of the equation of a circle centered at the origin is:
_x_2 + _y_2 = _r_2
We know that the radius of our circle is five. Therefore, we know that the equation for our circle is:
_x_2 + _y_2 = 52
_x_2 + _y_2 = 25
Now, the question asks for the positive y-coordinate when x = 2. To solve this, simply plug in for x:
22 + _y_2 = 25
4 + _y_2 = 25
_y_2 = 21
y = ±√(21)
Since our answer will be positive, it must be √(21).
Solve for x and y using the rules of quadrilateral
x=6, y=9
x=9, y=6
x=2, y=4
x=6, y=10
Explanation
By using the rules of quadrilaterals we know that oppisite sides are congruent on a rhombus. Therefore, we set up an equation to solve for x. Then we will use that number and substitute it in for x and solve for y.
Give the 



The parabola has no 
Explanation
Set 

The terms have a GCF of 2, so
The trinomial in parentheses can be FOILed out by noting that 

And you can divide both sides by 3 to get rid of the coefficient:
Set each of the linear binomials to 0 and solve for 
or
The parabola has as its two intercepts the points 

What is the center and radius of the circle indicated by the equation?
Explanation
A circle is defined by an equation in the format 
The center is indicated by the point 

In the equation 


Find the area of a circle with a diameter of 
Explanation
Write the formula for the area of a circle.
Substitute the diameter and solve.
Consider the lines described by the following two equations:
4y = 3x2
3y = 4x2
Find the vertical distance between the two lines at the points where x = 6.
36
21
12
44
48
Explanation
Since the vertical coordinates of each point are given by y, solve each equation for y and plug in 6 for x, as follows:

Taking the difference of the resulting y -values give the vertical distance between the points (6,27) and (6,48), which is 21.
If 


Explanation
The easiest identity to use here is:
Substituting in the given values we get:
Find the mode of the data set.
Explanation
The mode of a data set is the data point(s) that appear the most often.
In the data set for this problem, both 4 and 5 appear twice, and no other number appears more than twice.
So for this data set there are two modes, 4 and 5.
A square on the coordinate plane has as its vertices the points with coordinates 



Explanation
The equation of the circle on the coordinate plane with radius 

The figure referenced is below:

The center of the inscribed circle is the center of the square, which is where its diagonals intersect; this point is the common midpoint of the diagonals. The coordinates of the midpoint of the diagonal with endpoints at 


This point, 

Setting