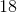3-Dimensional Geometry
Help Questions
SAT Math › 3-Dimensional Geometry
Find the surface area of a sphere with a radius of 3.
Explanation
Write the formula for the surface area of a sphere.
Substitute the radius into the equation.
The answer is:
A convex polyhedron has twenty faces and thirty-six vertices. How many edges does it have?
Explanation
The number of vertices 


Setting 

The polyhedron has 54 edges.
The slant height of a cone is 

Explanation
The formula for the surface area of a cone with base of radius 


The diameter of the base is 
Substitute in the surface area formula:
A convex polyhedron has twenty faces and thirty-six vertices. How many edges does it have?
Explanation
The number of vertices 


Setting 

The polyhedron has 54 edges.
The slant height of a cone is 

Explanation
The formula for the surface area of a cone with base of radius 


The diameter of the base is 
Substitute in the surface area formula:
Find the surface area of a sphere with a radius of 3.
Explanation
Write the formula for the surface area of a sphere.
Substitute the radius into the equation.
The answer is:
What is the volume of a regular tetrahedron with edges of 
Explanation
The volume of a tetrahedron is found with the formula:

where 
When 

What is the volume of a regular tetrahedron with edges of 
Explanation
The volume of a tetrahedron is found with the formula:

where 
When 

Which of the following numbers comes closest to the length of line segment in three-dimensional coordinate space whose endpoints are the origin and the point 
Explanation
Use the three-dimensional version of the distance formula:
The closest of the five choices is 7.
The surface area of cone 


Explanation
To figure out 




This equation can be reduced to:
For a normal right angle cone, 

so
Our 
The height of cone