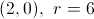Functions and Graphs
Help Questions
SAT Math › Functions and Graphs
What is the center and radius of the circle indicated by the equation?
Explanation
A circle is defined by an equation in the format 
The center is indicated by the point 

In the equation 


What is the vertex of 
Explanation
The polynomial is in standard form of a parabola.
To determine the vertex, first write the formula.
Substitute the coefficients.
Since the 
The answer is:
Which of the following is NOT a function?
Explanation
A function has to pass the vertical line test, which means that a vertical line can only cross the function one time. To put it another way, for any given value of 












Which of the following is NOT a function?
Explanation
A function has to pass the vertical line test, which means that a vertical line can only cross the function one time. To put it another way, for any given value of 












What is the center and radius of the circle indicated by the equation?
Explanation
A circle is defined by an equation in the format 
The center is indicated by the point 

In the equation 


Find the y-intercept of the following line.
Explanation
To find the y-intercept of any line, we must get the equation into the form
where m is the slope and b is the y-intercept.
To manipulate our equation into this form, we must solve for y. First, we must move the x term to the right side of our equation by subtracting it from both sides.
To isolate y, we now must divide each side by 3.
Now that our equation is in the desired form, our y-intercept is simply
Find the point at which these two lines intersect:
Explanation
We are looking for a point, 



Dividing both sides by 7, we isolate y.
Now, we can plug y back into either equation and solve for x.
Next, we can solve for x.
Therefore, the point where these two lines intersect is 
Find the equation of the line passing through the points 

Explanation
To calculate a line passing through two points, we first need to calculate the slope, 
Now that we have the slope, we can plug it into our equation for a line in slope intercept form.
To solve for 

Now that we have solved for b, we can plug that into our slope intercept form and produce and the answer
Give the 

Explanation
The 
is

Set 
The 


Give the 



The parabola has no 
Explanation
Set 

The terms have a GCF of 2, so
The trinomial in parentheses can be FOILed out by noting that 

And you can divide both sides by 3 to get rid of the coefficient:
Set each of the linear binomials to 0 and solve for 
or
The parabola has as its two intercepts the points