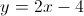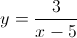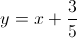Solving Linear Functions
Help Questions
SAT Math › Solving Linear Functions
Find the equation of the line passing through the points 

Explanation
To calculate a line passing through two points, we first need to calculate the slope, 
Now that we have the slope, we can plug it into our equation for a line in slope intercept form.
To solve for 

Now that we have solved for b, we can plug that into our slope intercept form and produce and the answer
Find the point at which these two lines intersect:
Explanation
We are looking for a point, 



Dividing both sides by 7, we isolate y.
Now, we can plug y back into either equation and solve for x.
Next, we can solve for x.
Therefore, the point where these two lines intersect is 
Solve:
Explanation
Distribute the right side.
Rewrite the equation.
Subtract 
Add 4 on both sides.
Divide by three on both sides.
The answer is:
Find the equation for the line goes through the two points below.
Explanation
Let 
First, calculate the slope between the two points.
Next, use the slope-intercept form to calculate the intercept. We are able to plug in our value for the slope, as well the the values for 
Using slope-intercept form, where we know 


If 

Explanation
A function of x equals five. This can be translated to:
This means that every point on the x-axis has a y value of five.
Therefore, 
The answer is:
Solve for 

Explanation
The first thing is to plug in the given value so you equation is

Then you must subtract 

You now have
and you must multiply by 

Solve for 

Explanation
First, subtract 7 to both sides.
Factor the y on the left hand side.
Divide both sides by 3 – x.
Take an extra step by factoring the minus sign on the denominator.
Cancel the minus signs.
Let 

Explanation
Substitute the fraction as 
Multiply the whole number with the numerator.
Convert the expression so that both terms have similar denominators.
The answer is:
Solve:
Explanation
Add 
Subtract 2 from both sides.
Divide by 10 on both sides.
Reduce the fractions.
The answer is:
If 

Explanation
Replace the value of negative two with the x-variable.
There is no need to use the FOIL method to expand the binomial.
The answer is: