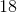SAT Subject Test in Math I

Help Questions

SAT Math › SAT Subject Test in Math I

Questions 1 - 10

Find the midpoint of the line that passes through the points and .

Explanation

Recall the midpoint formula as $(\frac{x1+x2}{2}, \frac{y1+y2}{2})$ .

Thus,

$(\frac{2+(-2)}{2},\frac{-1+1}{2}) = (0,0)$

Find the equation of the line passing through the points $\small (-3,2)$ and $\small (1,8)$ .

$\small y=\frac{3}{2}x+\frac{13}{2}$

$\small y=-\frac{3}{2}x+\frac{13}{2}$

$\small y=\frac{2}{3}x-\frac{13}{2}$

$\small y=\frac{2}{3}x+\frac{13}{2}$

$\small y=-\frac{2}{3}x+\frac{13}{2}$

Explanation

To calculate a line passing through two points, we first need to calculate the slope, $\small m$ .

$\small m=\frac{\Delta y}{\Delta x} =\frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{8-2}{1-(-3)} = \frac{6}{4} = \frac{3}{2}$

Now that we have the slope, we can plug it into our equation for a line in slope intercept form.

$\small y=\frac{3}{2}x+b$

To solve for $\small b$ , we can plug in one of the points we were given. For the sake of this example, let's use $\small (-3,2)$ , but realize either point will give use the same answer.

$\small 2=\frac{3}{2}(-3)+b$

$\small 2=\frac{-9}{2}+b$

$\small 2+\frac{9}{2} = b$

$\small \frac{13}{2} = b$

Now that we have solved for b, we can plug that into our slope intercept form and produce and the answer

$\small y=\frac{3}{2}x+\frac{13}{2}$

We have a square with length 2 sitting in the first quadrant with one corner touching the origin. If the square is inscribed inside a circle, find the equation of the circle.

Explanation

If the square is inscribed inside the circle, in means the center of the circle is at (1,1). We need to also find the radius of the circle, which happens to be the length from the corner of the square to it's center.

Now use the equation of the circle with the center and .

We get

Determine the exact value of .

$4\sqrt2$

$8\sqrt2$

$6\sqrt2$

$\frac{\sqrt2}{8}$

$\frac{\sqrt2}{4}$

Explanation

The exact value of is the x-value when the angle is 45 degrees on the unit circle.

The x-value of this angle is $\frac{\sqrt2}{2}$ .

$8cos(45)= 8\left(\frac{\sqrt{2}}{2}\right)=4\sqrt2$

Which of the following describes a triangle with sides one kilometer, 100 meters, and 100 meters?

The triangle cannot exist.

The triangle is acute and equilateral.

The triangle is obtuse and isosceles, but not equilateral.

The triangle is acute and isosceles, but not equilateral.

The triangle is obtuse and scalene.

Explanation

One kilometer is equal to 1,000 meters, so the triangle has sides of length 100, 100, and 1,000. However,

That is, the sum of the least two sidelengths is not greater than the third. This violates the Triangle Inequality, and this triangle cannot exist.

One line has four collinear points in order from left to right A, B, C, D. If AB = 10’, CD was twice as long as AB, and AC = 25’, how long is AD?

45'

40'

50'

35'

30'

Explanation

AB = 10 ’

BC = AC – AB = 25’ – 10’ = 15’

CD = 2 * AB = 2 * 10’ = 20 ’

AD = AB + BC + CD = 10’ + 15’ + 20’ = 45’

Solve the following function:

$11=x^{2}-5$

and

Explanation

You must get by itself so you must add to both side which results in

$16=x^{2}$ .

You must get the square root of both side to undue the exponent.

This leaves you with .

But since you square the in the equation, the original value you plug can also be its negative value since squaring it will make it positive anyway.

This means your answer can be or .

A convex polyhedron has twenty faces and thirty-six vertices. How many edges does it have?

Explanation

The number of vertices , edges , and faces of any convex polyhedron are related by By Euler's Formula:

Setting and solving for :

The polyhedron has 54 edges.

Find the y-intercept of the following line.

$\small 3$

$\small -12$

Explanation

To find the y-intercept of any line, we must get the equation into the form

where m is the slope and b is the y-intercept.

To manipulate our equation into this form, we must solve for y. First, we must move the x term to the right side of our equation by subtracting it from both sides.