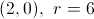Graphing Functions

Help Questions

SAT Math › Graphing Functions

Questions 1 - 10

Give the -intercept(s) of the parabola of the equation

$f(x) = 3x^{2}-9x -54$

and

$\left ( -\frac{3}{2}, 0 \right )$ and $\left ( \frac{3}{2}, 0 \right )$

and

The parabola has no -intercept.

Explanation

Set and solve for :

$f(x) = 3x^{2}-9x -54$

$3x^{2}-9x -54 = 0$

The terms have a GCF of 2, so

$3\left ( x^{2}- 3x - 18 \right )= 0$

The trinomial in parentheses can be FOILed out by noting that and $-6 \times 3= -18$ :

And you can divide both sides by 3 to get rid of the coefficient:

Set each of the linear binomials to 0 and solve for :

$x - 6 = 0 \Rightarrow x = 6$

$x +3= 0 \Rightarrow x = -3$

The parabola has as its two intercepts the points and .

Based on the figure below, which line depicts a quadratic function?

Red line

Blue line

Green line

Purple line

None of them

Explanation

A parabola is one example of a quadratic function, regardless of whether it points upwards or downwards.

The red line represents a quadratic function and will have a formula similar to $\small {f(x)=ax^2+bx+c}$ .

The blue line represents a linear function and will have a formula similar to $\small {f(x)=ax+b$ .

The green line represents an exponential function and will have a formula similar to $\small {f(x)=ax^b}$ .

The purple line represents an absolute value function and will have a formula similar to $\small {f(x)=\left |ax+b \right |}.$ .

Give the -coordinate of the vertex of the parabola of the function

$f(x) = 2x^{2} + 6x + 5$ .

$\frac{1}{2}$

$\frac{3}{2}$

$\frac{37}{2}$

Explanation

The -coordinate of the vertex of a parabola of the form

$f(x) = ax^{2}+ bx + c$

$x= -\frac{b}{2a}$ .

Set :

$x= -\frac{6}{2\cdot 2} = -\frac{6}{4} =- \frac{3}{2}$

The -coordinate is therefore $f\left (- \frac{3}{2} \right )$ :

$f(x) = 2x^{2} + 6x + 5$

$f \left ( -\frac{3}{2} \right )= 2\left ( -\frac{3}{2} \right )^{2}+ 6\left ( -\frac{3}{2} \right ) + 5$

$= 2\left ( \frac{9}{4} \right ) + 6\left (- \frac{3}{2} \right ) + 5$

$= \frac{9}{2} - 9 + 5 = \frac{1}{2}$ , which is the correct choice.

What is the center and radius of the circle indicated by the equation?

$(2,0),\ r=6$

$(-2,0),\ r=6$

$(2,0),\ r=36$

$(-2,0),\ r=36$

Explanation

A circle is defined by an equation in the format .

The center is indicated by the point and the radius .

In the equation , the center is and the radius is .

Consider the equation:

$y = 3x^{2} - 10x +5$

The vertex of this parabolic function would be located at:

$(\frac{5}{3}, \frac{-10}{3})$

$(\frac{-5}{3}, \frac{-10}{3})$

$(\frac{-5}{3}, 30)$

$(\frac{5}{3}, \frac{2}{25})$

$(\frac{5}{3}, \frac{27}{25})$

Explanation

For any parabola, the general equation is

$y = ax^{2} + bx +c$ , and the x-coordinate of its vertex is given by

$x = \frac{-b}{2a}$ .

For the given problem, the x-coordinate is

$x = \frac{-(-10)}{2(3)} = \frac{5}{3}$ .

To find the y-coordinate, plug $\frac{5}{3}$ into the original equation:

$y = 3(\frac{5}{3})^{2} - 10(\frac{5}{3}) +5 = \frac{-10}{3}$

Therefore the vertex is at $(\frac{5}{3}, \frac{-10}{3})$ .

Based on the figure below, which line depicts a quadratic function?

Red line

Blue line

Green line

Purple line

None of them

Explanation

A parabola is one example of a quadratic function, regardless of whether it points upwards or downwards.

The red line represents a quadratic function and will have a formula similar to $\small {f(x)=ax^2+bx+c}$ .

The blue line represents a linear function and will have a formula similar to $\small {f(x)=ax+b$ .

The green line represents an exponential function and will have a formula similar to $\small {f(x)=ax^b}$ .

The purple line represents an absolute value function and will have a formula similar to $\small {f(x)=\left |ax+b \right |}.$ .

Consider the equation:

$y = 3x^{2} - 10x +5$

The vertex of this parabolic function would be located at:

$(\frac{5}{3}, \frac{-10}{3})$

$(\frac{-5}{3}, \frac{-10}{3})$

$(\frac{-5}{3}, 30)$

$(\frac{5}{3}, \frac{2}{25})$

$(\frac{5}{3}, \frac{27}{25})$

Explanation

For any parabola, the general equation is

$y = ax^{2} + bx +c$ , and the x-coordinate of its vertex is given by

$x = \frac{-b}{2a}$ .

For the given problem, the x-coordinate is

$x = \frac{-(-10)}{2(3)} = \frac{5}{3}$ .

To find the y-coordinate, plug $\frac{5}{3}$ into the original equation:

$y = 3(\frac{5}{3})^{2} - 10(\frac{5}{3}) +5 = \frac{-10}{3}$

Therefore the vertex is at $(\frac{5}{3}, \frac{-10}{3})$ .

Which of the given functions has the greatest amplitude?

$2\sin(x)$

$\sin(4x)$

$\sin(x+3)$

$\sin\frac{2\pi }{3}(x+2)$

$\frac{1}{2}\sin(4x)$

Explanation

The amplitude of a function is the amount by which the graph of the function travels above and below its midline. When graphing a sine function, the value of the amplitude is equivalent to the value of the coefficient of the sine. Similarly, the coefficient associated with the x-value is related to the function's period. The largest coefficient associated with the sine in the provided functions is 2; therefore the correct answer is $2\sin(x)$ .

The amplitude is dictated by the coefficient of the trigonometric function. In this case, all of the other functions have a coefficient of one or one-half.

Determine where the graphs of the following equations will intersect.