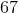Data Analysis and Statistics
Help Questions
SAT Math › Data Analysis and Statistics
A penny is altered so that the odds are 3 to 2 against it coming up tails when tossed; a nickel is altered so that the odds are 4 to 3 against it coming up tails when tossed. If both coins are tossed; what are the odds of both coins coming up heads?
23 to 12 against
23 to 12 in favor
29 to 6 in favor
29 to 6 against
Even
Explanation
3 to 2 odds in favor of heads is equal to a probability of 

Since the tosses of the two coins are independent, multiply the probabilities. The probability that there will be two heads is
This is 
Determine the mean:
Explanation
The mean is the average of all numbers in the data set.
Add the numbers, and divide the total sum by four, since there are four numbers.
The answer is:
Find the mode of the data set.
Explanation
The mode of a data set is the data point(s) that appear the most often.
In the data set for this problem, both 4 and 5 appear twice, and no other number appears more than twice.
So for this data set there are two modes, 4 and 5.

Above is the stem-and-leaf display for a group of test scores. Order the mean, the median, and the mode of the scores from least to greatest.
Mean, median, mode
Mean, mode, median
Mode, median, mean
Median, mean, mode
Median, mode, mean
Explanation
The scores represented can be found from matching the tens digits in the "stem" to the units digits that form the "leaves" in their row. For example, the "leaves" in the "5" row are "2 2 4 4 7 7 8", so the scores will be 52, 52, 54, 54, 57, 57, and 58.
There are 53 scores represented, so to find the median, look for the middle score, in position

As can be seen in this diagram, the score - the median - is 74.

The most frequently occurring "leaf" is the "6" in the "7" row, so the mode is 76.
The mean is the sum of the scores divided by 53. If we add the scores, we get

In ascending order, the values are mean, median, mode.

Above is the stem-and-leaf display for a group of test scores. Order the mean, the median, and the mode of the scores from least to greatest.
Mean, median, mode
Mean, mode, median
Mode, median, mean
Median, mean, mode
Median, mode, mean
Explanation
The scores represented can be found from matching the tens digits in the "stem" to the units digits that form the "leaves" in their row. For example, the "leaves" in the "5" row are "2 2 4 4 7 7 8", so the scores will be 52, 52, 54, 54, 57, 57, and 58.
There are 53 scores represented, so to find the median, look for the middle score, in position

As can be seen in this diagram, the score - the median - is 74.

The most frequently occurring "leaf" is the "6" in the "7" row, so the mode is 76.
The mean is the sum of the scores divided by 53. If we add the scores, we get

In ascending order, the values are mean, median, mode.
Determine the mean:
Explanation
The mean is the average of all numbers in the data set.
Add the numbers, and divide the total sum by four, since there are four numbers.
The answer is:
Find the mode of the data set.
Explanation
The mode of a data set is the data point(s) that appear the most often.
In the data set for this problem, both 4 and 5 appear twice, and no other number appears more than twice.
So for this data set there are two modes, 4 and 5.
A penny is altered so that the odds are 3 to 2 against it coming up tails when tossed; a nickel is altered so that the odds are 4 to 3 against it coming up tails when tossed. If both coins are tossed; what are the odds of both coins coming up heads?
23 to 12 against
23 to 12 in favor
29 to 6 in favor
29 to 6 against
Even
Explanation
3 to 2 odds in favor of heads is equal to a probability of 

Since the tosses of the two coins are independent, multiply the probabilities. The probability that there will be two heads is
This is 

Above is the stem-and-leaf display for a group of test scores. Which of the following scores would come closest to being at the 70th percentile?
Explanation
The stem-and-leaf display represents 53 scores. The score at the 70th percentile would be the score that is greater than 70% of the 53 scores, or
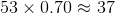
We count up 38 scores from the bottom:

The 38th-lowest score is 78, which is the correct choice.

Above is the stem-and-leaf display for a group of test scores. Which of the following scores would come closest to being at the 70th percentile?
Explanation
The stem-and-leaf display represents 53 scores. The score at the 70th percentile would be the score that is greater than 70% of the 53 scores, or
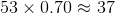
We count up 38 scores from the bottom:

The 38th-lowest score is 78, which is the correct choice.

![[13,5,8,-6]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/937387/gif.latex)