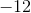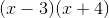Binomials
Help Questions
PSAT Math › Binomials
Give the coefficient of 

Explanation
If the expression 

or, equivalently, the coefficient of 
Therefore, the 

Give the coefficient of 

Explanation
If the expression 

or, equivalently, the coefficient of 
Therefore, the 
Give the coefficient of 

Explanation
While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two 
Add:
The correct response is -122.
Give the coefficient of 

Explanation
If the expression 

or, equivalently, the coefficient of 
Therefore, the 

Give the coefficient of 

Explanation
If the expression 

or, equivalently, the coefficient of 
Therefore, the 
Give the coefficient of 

Explanation
While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two 
Add:
The correct response is -122.
Give the coefficient of 

Explanation
While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two 
Add: 
The correct response is 
Give the coefficient of 

Explanation
If the expression 

or, equivalently, the coefficient of 
Therefore, the 

Give the coefficient of 

Explanation
While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two 
Add: 
The correct response is 
Multiply the binomial.
Explanation
By multiplying with the foil method, we multiply our first values giving